题目内容
10．数轴上A、B两点位于原点O的两侧，点A表示的实数是a，点B表示的实数是b，若|a-b|=2013，且AO=2BO，则a+b的值是（ ）| A． | 671 | B． | 2013 | C． | -671 | D． | ±671 |
分析 先根据AB两点之间的距离为2013，且AO=2BO求出AO及BO的长，进而得出a、b的值，故可得出结论．
解答 解：∵|a-b|=2013，且AO=2BO，
∴BO=$\frac{1}{3}$×2013=671，AO=2013-671=1342，
∵点A表示有理数a，点B表示有理数b，A、B分别在原点的两侧，
∴当B在原点左侧，A在原点右侧时，a+b=-671+1342=671；
当A在原点左侧，B在原点右侧时，a+b=-1342+671=-671．
故选：D．
点评 本题考查的是实数与数轴，熟知数轴上两点间距离的定义是解答此题的关键．
练习册系列答案
相关题目
如图，已知l1∥l2∥l3，AB=7，BC=8，DF=18，求EF的长．
18．下列事件中，是确定事件的是（ ）
| A． | 早上的太阳从西边升起 | |
| B． | 打开电视机，它正在播巴西世界杯 | |
| C． | 任意掷一枚质地均匀的骰子，掷出的点数是偶数 | |
| D． | 小明此次期末考试数学考了100分 |
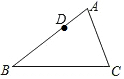在△ABC中，AB=6，AC=4，D是线段AB上的一点，且AD=2，若E是线段AC上的一点，且△ADE与△ABC相似，则AE=$\frac{4}{3}$或3．
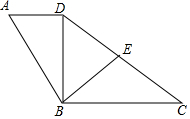已知：如图，在四边形ABCD中，AB=3，BC=4，AD∥BC，∠ADB=90°，cosA=$\frac{1}{3}$．