题目内容
4.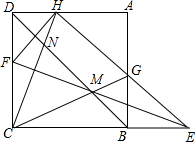 如图,已知正方形纸片ABCD,E为CB延长线上一点,F为边CD上一点,将纸片沿EF翻折,点C恰好落在AD边上的点H,连接BD,CH,CG.CH交BD于点N,EF、CG、BD恰好交于一点M.若DH=2,BG=3,则线段MN的长度为$\frac{5\sqrt{2}}{2}$.
如图,已知正方形纸片ABCD,E为CB延长线上一点,F为边CD上一点,将纸片沿EF翻折,点C恰好落在AD边上的点H,连接BD,CH,CG.CH交BD于点N,EF、CG、BD恰好交于一点M.若DH=2,BG=3,则线段MN的长度为$\frac{5\sqrt{2}}{2}$.
分析 作CP⊥HG于P,首先证明DH=HP,GP=BG,推出GH=5,设正方形边长为a,在Rt△AHG中利用勾股定理求出a,再由BG∥CD,得$\frac{BM}{DM}$=$\frac{BG}{CD}$=$\frac{3}{6}$=$\frac{1}{2}$,由DH∥CB,得$\frac{DN}{BN}$=$\frac{DH}{BC}$=$\frac{1}{3}$,分别求出BM、DN即可解决问题.
解答 解:作CP⊥HG于P,
∵四边形ABCD是正方形,
∴CD=BC,AD∥BC,∠CDA=90°,
∴∠DHC=∠HCE,
由翻折性质可知,∠ECH=∠EHC,
∴∠DHC=∠CHE,
∵CD⊥HD,CP⊥HE,
∴CP=CD=BC,
∴△CHD≌△CHP,△CGP≌△CGB,
∴DH=HP=2,PG=GB=3,
∴HG=2+3=5,
设正方形边长为a,在Rt△AHG中,∵HG2=AH2+AG2,
∴52=(a-2)2+(a-3)2,
∴a=6或-1(舍弃),
∴CD=BC=6,BD=6$\sqrt{2}$,
∵BG∥CD,
∴$\frac{BM}{DM}$=$\frac{BG}{CD}$=$\frac{3}{6}$=$\frac{1}{2}$,
∴BM=2$\sqrt{2}$,
∵DH∥CB,
∴$\frac{DN}{BN}$=$\frac{DH}{BC}$=$\frac{1}{3}$,
∴DN=$\frac{3}{2}$$\sqrt{2}$,
∴MN=BD-DN-BM=$\frac{5\sqrt{2}}{2}$.
故答案为$\frac{5\sqrt{2}}{2}$.
点评 本题考查翻折变换、正方形的性质、全等三角形的判定和性质、角平分线的性质、勾股定理、平行线分线段成比例定理等知识,解题的关键是学会添加辅助线,构造全等三角形解决问题,属于中考常考题型.

 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案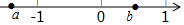 有理数a、b在数轴上对应的位置如图所示,则( )
有理数a、b在数轴上对应的位置如图所示,则( )| A. | a-b<0 | B. | a+b>0 | C. | a-b=0 | D. | a-b>0 |
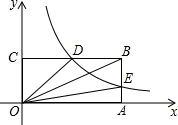 如图,在平面直角坐标系中,点O为坐标系原点,矩形OABC的边OA,OC分别在x轴和y轴上,其中OA=6,OC=3,已知反比例函数y=$\frac{k}{x}$(x>0)的图象经过BC边上的中点D,交AB于点E
如图,在平面直角坐标系中,点O为坐标系原点,矩形OABC的边OA,OC分别在x轴和y轴上,其中OA=6,OC=3,已知反比例函数y=$\frac{k}{x}$(x>0)的图象经过BC边上的中点D,交AB于点E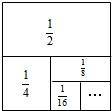 利用图形来表示数量或数量关系,也可以利用数量或数量关系来描述图形特征或图形之间的关系,这种思想方法称为数形结合.我们刚学过的第9章《整式乘法与因式分解》就很好地体现了这一思想方法,你能利用数形结合的思想解决下列问题吗?
利用图形来表示数量或数量关系,也可以利用数量或数量关系来描述图形特征或图形之间的关系,这种思想方法称为数形结合.我们刚学过的第9章《整式乘法与因式分解》就很好地体现了这一思想方法,你能利用数形结合的思想解决下列问题吗?