题目内容
15.已知:a+b=4,ab=1.求:①?a2+b2的值;
?②a-b的值.
分析 ①先根据完全平方公式进行变形,再整体代入求出即可
②利用完全平方公式列出关系式,把a+b与ab的值代入,开方即可求出a-b的值.
解答 解:①∵a+b=4,ab=1,
∴a2+b2
=(a+b)2-2ab
=42-2×1=14;
②∵a+b=4,ab=1,
∴(a-b)2=(a+b)2-4ab=16-4=12,
则a-b=±2$\sqrt{3}$.
点评 本题考查了完全平方公式的应用,能熟记公式是解此题的关键,注意:完全平方公式是(a±b)2=a2±2ab+b2.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案
相关题目
5.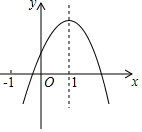 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为x=1,下列结论中正确的是( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为x=1,下列结论中正确的是( )
 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为x=1,下列结论中正确的是( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为x=1,下列结论中正确的是( )| A. | ab>0 | B. | b=2a | C. | 4a+2b+c<0 | D. | a+c<b |
 如图,在Rt△ABC中,∠BAC=90°.将Rt△ABC绕点C按逆时针方向旋转48°得到Rt△A′B′C,点A在边B′C上,则∠B′的大小为42°.
如图,在Rt△ABC中,∠BAC=90°.将Rt△ABC绕点C按逆时针方向旋转48°得到Rt△A′B′C,点A在边B′C上,则∠B′的大小为42°.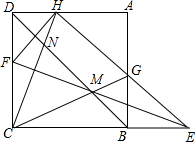 如图,已知正方形纸片ABCD,E为CB延长线上一点,F为边CD上一点,将纸片沿EF翻折,点C恰好落在AD边上的点H,连接BD,CH,CG.CH交BD于点N,EF、CG、BD恰好交于一点M.若DH=2,BG=3,则线段MN的长度为$\frac{5\sqrt{2}}{2}$.
如图,已知正方形纸片ABCD,E为CB延长线上一点,F为边CD上一点,将纸片沿EF翻折,点C恰好落在AD边上的点H,连接BD,CH,CG.CH交BD于点N,EF、CG、BD恰好交于一点M.若DH=2,BG=3,则线段MN的长度为$\frac{5\sqrt{2}}{2}$.