题目内容
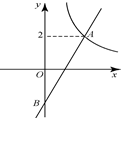
如图,反比例函数y= (k>0)与矩形OABC在第一象限相交于D、E两点,OA=2,OC=4,连接OD、OE、DE.记△OAD、△OCE的面积分别为S、S .
(k>0)与矩形OABC在第一象限相交于D、E两点,OA=2,OC=4,连接OD、OE、DE.记△OAD、△OCE的面积分别为S、S .

(1)①点B的坐标为 ;②S S(填“>”、“<”、“=”);
(2)当点D为线段AB的中点时,求k的值及点E的坐标;
(3)当S+S=2时,试判断△ODE的形状,并求△ODE的面积.
 (k>0)与矩形OABC在第一象限相交于D、E两点,OA=2,OC=4,连接OD、OE、DE.记△OAD、△OCE的面积分别为S、S .
(k>0)与矩形OABC在第一象限相交于D、E两点,OA=2,OC=4,连接OD、OE、DE.记△OAD、△OCE的面积分别为S、S .
(1)①点B的坐标为 ;②S S(填“>”、“<”、“=”);
(2)当点D为线段AB的中点时,求k的值及点E的坐标;
(3)当S+S=2时,试判断△ODE的形状,并求△ODE的面积.
(1)点B的坐标为(4,2),= (2)k的值为4,点E的坐标为(4,1) (3)△ODE为直角三角形,

试题分析:(1)矩形OABC,AB=OC,BC=OA;OA=2,OC=4,B点在第一象限
所以点B的坐标为(4,2);反比例函数y=
 (k>0)与矩形OABC在第一象限相交于D、E两点,设D、E两点的坐标分别为
(k>0)与矩形OABC在第一象限相交于D、E两点,设D、E两点的坐标分别为 ,得
,得 ;D、E在第一象限, 记△OAD、△OCE的面积分别为S、S,
;D、E在第一象限, 记△OAD、△OCE的面积分别为S、S, ,所以S=S
,所以S=S (2)当点D为线段AB的中点时,D点的坐标(2,2),由(1)知
 ,解得k="4;"
,解得k="4;"  ,所以点E的坐标为(4,1)
,所以点E的坐标为(4,1) (3) 当S+S=2时,由(1)得
 ;S="1;"
;S="1;"  ;
; ;在矩形OABC,BD=AB-AD=3;BE=BC-CE=
;在矩形OABC,BD=AB-AD=3;BE=BC-CE= ;
; 都是直角三角形,由勾股定理得
都是直角三角形,由勾股定理得
∵

∴ODE为直角三角形,

∴S
 =
= OD·DE=
OD·DE=  ×
× ×
× =
=
点评:本题考查反比例函数,矩形,勾股定理,解本题需要熟悉反比例函数的性质,矩形的性质,掌握勾股定理的内容

练习册系列答案
相关题目
 与
与 是反比例函数
是反比例函数 图象上的两个点。
图象上的两个点。
 的值;
的值; ,点
,点 是反比例函数
是反比例函数 四点为顶点的四边形为梯形,请你求出点
四点为顶点的四边形为梯形,请你求出点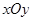 中,函数
中,函数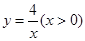 的图象与一次函数
的图象与一次函数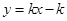 的图象的交点为
的图象的交点为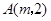 .
.
 轴交于点
轴交于点 ,若
,若 是
是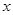 轴上一点,且满足
轴上一点,且满足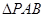 的面积是4,求点
的面积是4,求点 (k≠0)的图象经过点(-2,8).
(k≠0)的图象经过点(-2,8).
 中,
中, ,
, .
. ,设
,设 ,
, ,则
,则 与
与 之间的函数关系式为 .
之间的函数关系式为 .
 、
、 、
、 在双曲线
在双曲线 上,
上, 轴于
轴于 ,
,  轴于
轴于 ,点
,点 在
在 轴上,且
轴上,且 , 则图中阴影部分的面积之为 .
, 则图中阴影部分的面积之为 .
 在
在 轴上,
轴上, ,点
,点 的坐标为
的坐标为 ,将
,将 绕点
绕点 ,点
,点 的对应
的对应 恰好落在双曲线
恰好落在双曲线 上,则
上,则 的值为
的值为
 .
. .
. .
. .
. 的图象上,则y1、y2、y3的大小关系为 (用“>”连接)
的图象上,则y1、y2、y3的大小关系为 (用“>”连接)