题目内容
14. 如图,在△ABC中,P为AB上的一点,在下列条件中:
如图,在△ABC中,P为AB上的一点,在下列条件中:①∠ACP=∠B;②AC2=AP•PB;③∠APC=∠ACB;④AB•CP=AP•CB,
能满足△APC∽△ACB的条件是①②③.
分析 根据相似三角形的判定方法对各个条件进行分析,从而得到最后答案.
解答 解:∵∠A=∠A
∴①∠ACP=∠B,③∠APC=∠ACB时都相似;
∵AC2=AP•AB
∴AC:AB=AP:AC
∴②相似;
④此两个对应边的夹角不是∠A,所以不相似.
所以能满足△APC与△ACB相似的条件是①②③.
故答案为:①②③.
点评 本题考查的是相似三角形的判定,熟知有两组角对应相等的两个三角形相似是解答此题的关键.

练习册系列答案
相关题目
6.一个数的相反数不比它本身大,则这个数为( )
| A. | 正数 | B. | 负数 | C. | 非正数 | D. | 非负数 |
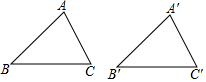 ①已知AB=A′B′,BC=B′C′,那只要再知道∠B=∠B′,就可以根据“SAS”得到△ABC≌△A′B′C′.
①已知AB=A′B′,BC=B′C′,那只要再知道∠B=∠B′,就可以根据“SAS”得到△ABC≌△A′B′C′.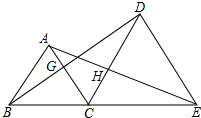 如图,已知△ABC和△DCE都是等边三角形(三边都相等,三个角都是60°),且B,C,E在同一直线上,连接BD交AC于点G,连接AE交CD于点H.求证:
如图,已知△ABC和△DCE都是等边三角形(三边都相等,三个角都是60°),且B,C,E在同一直线上,连接BD交AC于点G,连接AE交CD于点H.求证: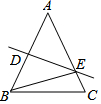 ①若△ABC中,AB=AC=10,DE垂直平分AB交AC于E,且△BEC的周长是16,△ABC的周长26.
①若△ABC中,AB=AC=10,DE垂直平分AB交AC于E,且△BEC的周长是16,△ABC的周长26.