Question

4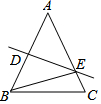．①若△ABC中，AB=AC=10，DE垂直平分AB交AC于E，且△BEC的周长是16，△ABC的周长26．
②若△ABC中，AB=AC，DE垂直平分AB交AC于E，且∠A=45°，求∠BED=45°，∠EBC=22.5°．

Answer 1

分析 （1）先根据DE垂直平分AB交AC于E，得出AE=BE，再根据△BEC的周长是16，得出AE+CE+BC=16，最后计算△ABC的周长；
（2）先根据DE垂直平分AB交AC于E，得出AE=BE，∠A=∠DBE=45°，再根据AB=AC，∠A=45°，得出∠ABC=67.5°，最后计算得出∠EBC即可．

解答 解：①∵DE垂直平分AB交AC于E，
∴AE=BE，
∵△BEC的周长是16，
∴BE+CE+BC=16，
∴AE+CE+BC=16，
∵AB=AC=10，
∴AB+AC+BC=26；
②∵DE垂直平分AB交AC于E，
∴AE=BE，
∴∠A=∠DBE=45°，
∴∠BED=90°-45°=45°，
∵AB=AC，∠A=45°，
∴∠ABC=67.5°，
∴∠EBC=67.5°-45°=22.5°．
故答案为：26，45°，22.5°．

点评 本题主要考查了垂直平分线的性质以及等腰三角形的性质的运用，解决问题的关键是掌握：垂直平分线上任意一点，到线段两端点的距离相等．