题目内容
18.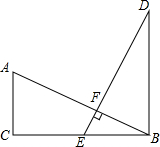 如图,已知AC⊥CB,DB⊥CB,AB⊥DE,AB=DE,E是BC的中点.
如图,已知AC⊥CB,DB⊥CB,AB⊥DE,AB=DE,E是BC的中点.(1)观察并猜想BD和BC有何数量关系?并证明你猜想的结论.
(2)若BD=6cm,求AB的长.
分析 (1)结论:BD=BC.只要证明△ABC≌△EDB即可解决问题.
(2)在Rt△DEB中,求出DE,理由全等三角形的性质AB=DE即可解决问题;
解答 解:(1)结论:BD=BC.
理由:∵AC⊥CB,DB⊥CB,AB⊥DE
∴∠C=∠CBD=∠EFB=90°,
∴∠ABC+∠A=90°,∠ABC+∠DEB=90°
所以∠DEB=∠A,
又AB=DE
在△ABC和△EDB中,
$\left\{\begin{array}{l}{∠C=∠DBE}\\{∠A=∠DEB}\\{AB=DE}\end{array}\right.$,
∴△ABC≌△EDB
∴BD=BC.
(2)∵BD=6cm∴BC=6cm
E是BC的中点.
BE=3cm
在Rt△BDE中,$DE=\sqrt{B{D^2}+B{E^2}}=\sqrt{36+9}=3\sqrt{5}$,
∴AB=DE=$3\sqrt{5}(cm)$.
点评 本题考查全等三角形的判定和性质、勾股定理等知识,解题的关键是熟练掌握基本知识,灵活运用所学知识解决问题,属于中考常考题型.

练习册系列答案
相关题目
9.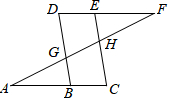 如图,点E在直线DF上,点B在直线AC上,若∠AGB=∠EHF,∠C=∠D,则∠A与∠F的大小关系是( )
如图,点E在直线DF上,点B在直线AC上,若∠AGB=∠EHF,∠C=∠D,则∠A与∠F的大小关系是( )
 如图,点E在直线DF上,点B在直线AC上,若∠AGB=∠EHF,∠C=∠D,则∠A与∠F的大小关系是( )
如图,点E在直线DF上,点B在直线AC上,若∠AGB=∠EHF,∠C=∠D,则∠A与∠F的大小关系是( )| A. | ∠A+∠F=90° | B. | ∠A>∠F | C. | ∠A<∠F | D. | ∠A=∠F |
10.若a<b<0,则下列各式错误的是( )
| A. | a-2<b-2 | B. | $-\frac{a}{5}<-\frac{b}{5}$ | C. | $\frac{1}{a}>\frac{1}{b}$ | D. | 2a-1<2b-1 |

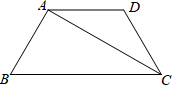 如图,AD∥BC,AC是∠BCD的平分线,∠BCD=60°,∠BAD=120°.
如图,AD∥BC,AC是∠BCD的平分线,∠BCD=60°,∠BAD=120°. 如图,一渔船由西往东航行,在A点测得海岛C位于北偏东60°的方向,前进20海里到达B点,此时,测得海岛C位于北偏东45°的方向,请求出海岛C到航线AB的距离(结果保留根号).
如图,一渔船由西往东航行,在A点测得海岛C位于北偏东60°的方向,前进20海里到达B点,此时,测得海岛C位于北偏东45°的方向,请求出海岛C到航线AB的距离(结果保留根号).