题目内容
5．
如图，一渔船由西往东航行，在A点测得海岛C位于北偏东60°的方向，前进20海里到达B点，此时，测得海岛C位于北偏东45°的方向，请求出海岛C到航线AB的距离（结果保留根号）．
分析 作CD⊥AB于D，设CD=x海里，根据正切的概念表示出BD、AD，根据题意列出方程，解方程即可．
解答 解：
作CD⊥AB于D，
设CD=x海里，
在Rt△CBD中，∠CBD=45°，
∴BD=CD=x，
在Rt△ABD中，AD=$\frac{CD}{tan∠CAD}$=$\sqrt{3}$x，
则x+20=$\sqrt{3}$x，
解得，x=10$\sqrt{3}$+10，
答：海岛C到航线AB的距离为（10$\sqrt{3}$+10）海里．
点评 本题考查的是解直角三角形的应用，掌握锐角三角函数的概念、正确标注方向角是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
13．下列关于整式的运算结果正确的是（ ）
| A． | 2x•（-xy）2=-2x3y | B． | （-x2）3÷（-x3）2=1 | ||
| C． | （$\frac{3}{4}$a3-$\frac{1}{2}$b）•2ab=$\frac{3}{2}$a4b-ab2 | D． | （3m-1）2=9m2-1 |
14．
如图，直线a、b被直线c所截，互为同旁内角是（ ）
如图，直线a、b被直线c所截，互为同旁内角是（ ）| A． | ∠4和∠6 | B． | ∠2和∠7 | C． | ∠4和∠5 | D． | ∠4和∠6 |
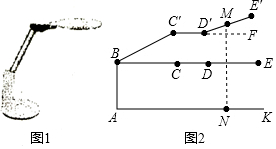市场上一款护眼灯（如图1），采用圆形面光源技术，胡烈其旋转支架等的宽度，得到它的侧面简化结构图（如图2），底座AB⊥桌面AK，旋转支架BC可绕点B旋转，转接头CD∥桌面AK，圆形面光源在旋转支架所在平面捏可绕点D旋转，其直径DE为20cm，若旋转支架旋转至BC′处，圆形面光源DE旋转至D′E′处，此时圆形面光源中心M到桌面的距离MN=40cm，已知AB=20cm，∠CBC=37°，∠E′D′F=24°，则旋转支架BC长为（ ）cm（结果精确到1cm，参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75，sin24°≈0.40，cos24°≈0.91，tan24°≈0.45）
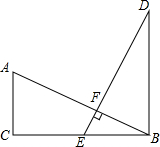如图，已知AC⊥CB，DB⊥CB，AB⊥DE，AB=DE，E是BC的中点．
10．
如图，OE平分∠AOC，OF平分∠BOC，且∠BOC=60°，若∠AOC+∠EOF=156°，则∠EOF的度数是（ ）
如图，OE平分∠AOC，OF平分∠BOC，且∠BOC=60°，若∠AOC+∠EOF=156°，则∠EOF的度数是（ ）| A． | 88° | B． | 30° | C． | 32° | D． | 48° |
17．在下列图形中，是中心对称图形而不是轴对称图形的是（ ）
| A． | 圆 | B． | 等边三角形 | C． | 梯形 | D． | 平行四边形 |
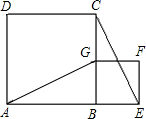如图，正方形BEFG的边BG在正方形ABCD的边BC上，连结AG，EC．