题目内容
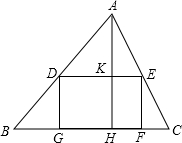已知△ABC的内接正方形DGFE，AH⊥BC于H，AH=5，AD：BD=2：3，求BC长．考点：相似三角形的判定与性质,正方形的性质
专题：
分析：求出KH的值，得出DE，证△ADE∽△ABC，得出比例式，代入求出即可．
解答：解：∵AD：BD=2：3，
∴
=
，
∵四边形DGFE是正方形，AH⊥BC，
∴DE=DG=KH=EF=GF，DE∥BC，
∴AH⊥DE，
∵DE∥BC，
∴
=
=
，
∵AH=5，
∴AK=2，KH=5-2=3，
即DE=3，
∵DE∥BC，
∴△ADE∽△ABC，
∴
=
，
∴
=
，
∴BC=7.5．
∴
| AD |
| AB |
| 2 |
| 5 |
∵四边形DGFE是正方形，AH⊥BC，
∴DE=DG=KH=EF=GF，DE∥BC，
∴AH⊥DE，
∵DE∥BC，
∴
| AD |
| AB |
| AK |
| AH |
| 2 |
| 5 |
∵AH=5，
∴AK=2，KH=5-2=3，
即DE=3，
∵DE∥BC，
∴△ADE∽△ABC，
∴
| DE |
| BC |
| AD |
| AB |
∴
| 3 |
| BC |
| 2 |
| 5 |
∴BC=7.5．
点评：本题考查了正方形的性质，相似三角形的性质和判定，平行线分线段成比例定理的应用，主要考查学生综合运用性质进行推理和计算的能力．
练习册系列答案
轻松暑假总复习系列答案
相关题目
如图，已知△ABC在坐标平面内的顶点C（2，0），∠ACB=90°，∠B=30°，AB=6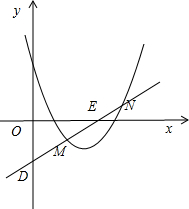
如图，已知抛物线y=x2-4x+3，过点D（0，-
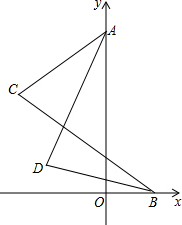如图，BD平分∠OBC，AD平分∠OAC，∠C=80°，求∠D的大小．