题目内容
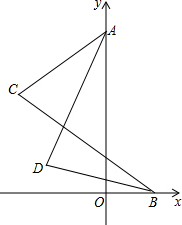 如图,BD平分∠OBC,AD平分∠OAC,∠C=80°,求∠D的大小.
如图,BD平分∠OBC,AD平分∠OAC,∠C=80°,求∠D的大小.考点:三角形内角和定理,三角形的外角性质
专题:
分析:先设∠CAD=∠1,∠OAD=∠2,∠CBD=∠3,∠OBD=∠4,根据已知和外角的性质得出∠AEB=∠C+2∠1和∠AEB=∠AOB+2∠3,从而得出∠1-∠3=
(∠AOB-∠C),再根据外角的性质得出∠CFD=∠C+∠1,∠CFD=∠D+∠3,最后根据∠C=80,即可得出答案.
| 1 |
| 2 |
解答: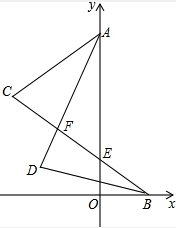 解:设∠CAD=∠1,∠OAD=∠2,∠CBD=∠3,∠OBD=∠4,
解:设∠CAD=∠1,∠OAD=∠2,∠CBD=∠3,∠OBD=∠4,
∵AD平分∠OAC,
∴∠1=∠2,∠OAC=2∠1,
∴∠AEB=∠C+∠OAC=∠C+2∠1,
∵BD平分∠OBC,
∴∠3=∠4,∠OBC=2∠3,
∴∠AEB=∠AOB+∠OBC=∠AOB+2∠3,
∴∠C+2∠1=∠AOB+2∠3,
∴∠1-∠3=
(∠AOB-∠C),
∵∠CFD=∠C+∠1,∠CFD=∠D+∠3,
∴∠C+∠1=∠D+∠3,
∴∠1-∠3=∠D-∠C,
∴∠D-∠C=
(∠AOB-∠C),
∴∠D=
(∠AOB+∠C),
∵∠AOB=90,∠C=80,
∴∠D=
(90+80)=85°.
 解:设∠CAD=∠1,∠OAD=∠2,∠CBD=∠3,∠OBD=∠4,
解:设∠CAD=∠1,∠OAD=∠2,∠CBD=∠3,∠OBD=∠4,∵AD平分∠OAC,
∴∠1=∠2,∠OAC=2∠1,
∴∠AEB=∠C+∠OAC=∠C+2∠1,
∵BD平分∠OBC,
∴∠3=∠4,∠OBC=2∠3,
∴∠AEB=∠AOB+∠OBC=∠AOB+2∠3,
∴∠C+2∠1=∠AOB+2∠3,
∴∠1-∠3=
| 1 |
| 2 |
∵∠CFD=∠C+∠1,∠CFD=∠D+∠3,
∴∠C+∠1=∠D+∠3,
∴∠1-∠3=∠D-∠C,
∴∠D-∠C=
| 1 |
| 2 |
∴∠D=
| 1 |
| 2 |
∵∠AOB=90,∠C=80,
∴∠D=
| 1 |
| 2 |
点评:此题考查了三角形内角和定理和三角形的外角的性质,关键是根据角平分线的性质和外角的性质得出∠AEB∠C+2∠1和∠AEB=∠AOB+2∠3.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
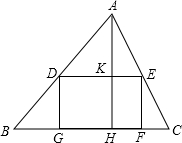 已知△ABC的内接正方形DGFE,AH⊥BC于H,AH=5,AD:BD=2:3,求BC长.
已知△ABC的内接正方形DGFE,AH⊥BC于H,AH=5,AD:BD=2:3,求BC长. 如图,在△ABC中,∠C=90°,∠B=28°,以C为圆心,CA为半径的圆交AB于点D,交BC于点E,则弧AD的度数为
如图,在△ABC中,∠C=90°,∠B=28°,以C为圆心,CA为半径的圆交AB于点D,交BC于点E,则弧AD的度数为