题目内容
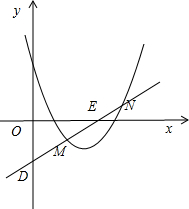 如图,已知抛物线y=x2-4x+3,过点D(0,-
如图,已知抛物线y=x2-4x+3,过点D(0,-| 5 |
| 2 |
考点:抛物线与x轴的交点
专题:
分析:设直线MN的解析式为y=kx-
(k≠0).根据一元二次方程x2-4x+3=0的根求得点E的坐标.把点E的坐标代入求得k的值即可.
| 5 |
| 2 |
解答:解:过点D(0-
)的直线与抛物线交于M(xM,yM)、N(xN,yN)两点,与x轴交于点E,使得M、N两点关于点E对称.
设直线MN的解析式为:y=kx-
,
则有:YM+YN=0,(6分)
由
,
x2-4x+3=kx-
,
移项后合并同类项得x2-(k+4)x+
=0,
∴xM+xN=4+k.
∴yM+yN=kxM-
+kxN-
=k(xM+xN)-5=0,
∴yM+yN=k(xM+xN)=5,
即k(k+4)-5=0,
∴k=1或k=-5.
当k=-5时,方程x2-(k+4)x+
=0的判别式△<0,直线MN与抛物线无交点,
∴k=1,
∴直线MN的解析式为y=x-
.
| 5 |
| 2 |
设直线MN的解析式为:y=kx-
| 5 |
| 2 |
则有:YM+YN=0,(6分)
由
|
x2-4x+3=kx-
| 5 |
| 2 |
移项后合并同类项得x2-(k+4)x+
| 11 |
| 2 |
∴xM+xN=4+k.
∴yM+yN=kxM-
| 5 |
| 2 |
| 5 |
| 2 |
∴yM+yN=k(xM+xN)=5,
即k(k+4)-5=0,
∴k=1或k=-5.
当k=-5时,方程x2-(k+4)x+
| 11 |
| 2 |
∴k=1,
∴直线MN的解析式为y=x-
| 5 |
| 2 |
点评:本题考查了抛物线与x轴的交点.此题根据中点坐标的性质求得点E的坐标是解题的关键.

练习册系列答案
相关题目
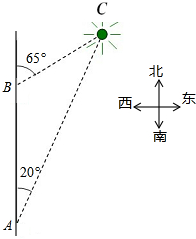 如图,一艘船以每小时32海里的速度向正北航行,在A处观察到灯塔C在船的北偏东20°方向上,半个小时后船航行到B处,在B处观测到灯塔C在船的北偏东65°的方向上.求灯塔C与B处之间的距离.
如图,一艘船以每小时32海里的速度向正北航行,在A处观察到灯塔C在船的北偏东20°方向上,半个小时后船航行到B处,在B处观测到灯塔C在船的北偏东65°的方向上.求灯塔C与B处之间的距离.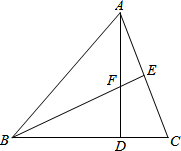 已知,△ABC中,AB=CB,AD⊥BC于D,AD=BD,CD=FD,BF的延长线交AC于E.求证:
已知,△ABC中,AB=CB,AD⊥BC于D,AD=BD,CD=FD,BF的延长线交AC于E.求证: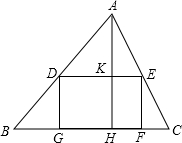 已知△ABC的内接正方形DGFE,AH⊥BC于H,AH=5,AD:BD=2:3,求BC长.
已知△ABC的内接正方形DGFE,AH⊥BC于H,AH=5,AD:BD=2:3,求BC长.