题目内容
 如图,已知△ABC在坐标平面内的顶点C(2,0),∠ACB=90°,∠B=30°,AB=6
如图,已知△ABC在坐标平面内的顶点C(2,0),∠ACB=90°,∠B=30°,AB=6| 2 |
①求A、B的坐标;
②求AB中点M的坐标.
考点:勾股定理,坐标与图形性质,含30度角的直角三角形,等腰直角三角形
专题:
分析:①过A作AE⊥x轴于点E,过B作BD⊥x轴于点D,先解直角△ABC,得到AC=
AB=3
,BC=
AC=3
,再由△BCD是等腰直角三角形得出CD=BD=
BC=3
,由△ACE是等腰直角三角形得出AE=CE=
AC=3,再根据C的坐标为(2,0),即可求出A、B的坐标;
②由A、B两点的坐标,根据中点坐标公式即可求出AB中点M的坐标.
| 1 |
| 2 |
| 2 |
| 3 |
| 6 |
| ||
| 2 |
| 3 |
| ||
| 2 |
②由A、B两点的坐标,根据中点坐标公式即可求出AB中点M的坐标.
解答: 解:①过A作AE⊥x轴于点E,过B作BD⊥x轴于点D.
解:①过A作AE⊥x轴于点E,过B作BD⊥x轴于点D.
在△ABC中,∵∠ACB=90°,∠B=30°,AB=6
,
∴AC=
AB=3
,BC=
AC=3
.
在△BCD中,∵∠BDC=90°,∠BCD=45°,
∴∠BCD=45°,
∴CD=BD=
BC=3
.
在△ACE中,∵∠AEC=90°,∠ACE=45°,
∴AE=CE=
AC=3.
∵C(2,0),
∴OC=2,
∴OE=CE-OC=1,
∴A点坐标为(-1,3).
∵OD=OC+CD=2+3
,
∴B的坐标(2+3
,3
);
②∵A(-1,3),B(2+3
,3
),
∴AB中点M的坐标为(
,
).
 解:①过A作AE⊥x轴于点E,过B作BD⊥x轴于点D.
解:①过A作AE⊥x轴于点E,过B作BD⊥x轴于点D.在△ABC中,∵∠ACB=90°,∠B=30°,AB=6
| 2 |
∴AC=
| 1 |
| 2 |
| 2 |
| 3 |
| 6 |
在△BCD中,∵∠BDC=90°,∠BCD=45°,
∴∠BCD=45°,
∴CD=BD=
| ||
| 2 |
| 3 |
在△ACE中,∵∠AEC=90°,∠ACE=45°,
∴AE=CE=
| ||
| 2 |
∵C(2,0),
∴OC=2,
∴OE=CE-OC=1,
∴A点坐标为(-1,3).
∵OD=OC+CD=2+3
| 3 |
∴B的坐标(2+3
| 3 |
| 3 |
②∵A(-1,3),B(2+3
| 3 |
| 3 |
∴AB中点M的坐标为(
1+3
| ||
| 2 |
3+3
| ||
| 2 |
点评:本题考查了解直角三角形,坐标与图形性质,含30度角的直角三角形的性质,等腰直角三角形的判定与性质,线段中点坐标公式,综合性较强,难度适中.

练习册系列答案
相关题目
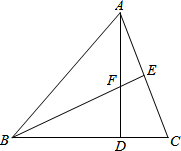 已知,△ABC中,AB=CB,AD⊥BC于D,AD=BD,CD=FD,BF的延长线交AC于E.求证:
已知,△ABC中,AB=CB,AD⊥BC于D,AD=BD,CD=FD,BF的延长线交AC于E.求证: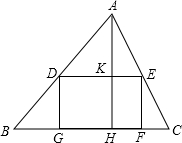 已知△ABC的内接正方形DGFE,AH⊥BC于H,AH=5,AD:BD=2:3,求BC长.
已知△ABC的内接正方形DGFE,AH⊥BC于H,AH=5,AD:BD=2:3,求BC长.