题目内容
19.如图,在平面直角坐标系xOy内,正方形AOBC顶点C的坐标为(2,2),过点B的直线∥OC,P是直线上一个动点,抛物线y=ax2+bx过O、C、P三点.(1)填空:直线的函数解析式为y=x-2;a,b的关系式是2a+b=1.
(2)当△PBC是等腰Rt△时,求抛物线的解析式;
(3)当抛物线的对称轴与正方形有交点时,直接写出点P横坐标x的取值范围$1-\sqrt{5}$≤x≤$1+\sqrt{5}$,且x≠0和2.
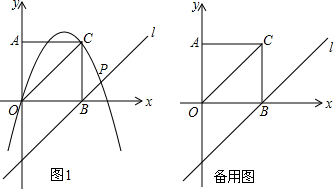
分析 (1)根据题意求得B(2,0)和直线OC的解析式为y=x,设直线l的解析式为y=x+b,根据待定系数法即可求得直线的函数解析式,把C的坐标代入y=ax2+bx即可求得a,b的关系式;
(2)分两种情况求得P的坐标,利用待定系数法即可求得;
(3)求得抛物线是顶点为C时的抛物线的解析式求得与直线l的交点坐标即可求得符合题意的点P横坐标x的取值范围.
解答 解:(1)∵正方形AOBC顶点C的坐标为(2,2),
∴B(2,0),
∵直线OC的解析式y=x,
∴设直线l的解析式为y=x+b,
∴0=2+b,
∴b=-2,
∴直线l的函数解析式为y=x-2,
把(2,2)代入y=ax2+bx得,2=4a+2b
∴2a+b=1;
(2)当∠BCP=90°时,则P的坐标为(4,2),如图2,
把C(2,2),P(4,2)代入y=ax2+bx得$\left\{\begin{array}{l}{4a+2b=2}\\{16a+4b=2}\end{array}\right.$,
解$\left\{\begin{array}{l}{a=-\frac{1}{4}}\\{b=\frac{3}{2}}\end{array}\right.$,
∴抛物线的解析式为y=-$\frac{1}{4}$x2+$\frac{3}{2}$x;
当∠BPC=90°时,则P的坐标为(3,1),如图3,
把C(2,2),P(3,1)代入y=ax2+bx得$\left\{\begin{array}{l}{4a+2b=2}\\{9a+3b=1}\end{array}\right.$
解得$\left\{\begin{array}{l}{a=-\frac{2}{3}}\\{b=\frac{7}{3}}\end{array}\right.$,
∴抛物线的解析式为$y=-\frac{2}{3}{x^2}+\frac{7}{3}x$;
(3)当抛物线的顶点为C时,如图4,
∴-$\frac{b}{2a}$=2,
∴b=-4a,
∵2a+b=1,
∴a=-$\frac{1}{2}$,b=2,
∴抛物线的解析式为y=-$\frac{1}{2}$x2+2x,
解$\left\{\begin{array}{l}{y=-\frac{1}{2}{x}^{2}+2x}\\{y=x-2}\end{array}\right.$得x=1±$\sqrt{5}$,
∴点P横坐标x的取值范围$1-\sqrt{5}$≤x≤$1+\sqrt{5}$,且x≠0和2.
故答案为:y=x-2,2a+b=1,$1-\sqrt{5}$≤x≤$1+\sqrt{5}$,且x≠0和2.
点评 本题是二次函数的综合题,考查了待定系数法求二次函数的解析式、等腰直角三角形的性质、抛物线和直线的交点以及分类讨论思想的运用等,熟练掌握待定系数法是解题的关键.

 阅读快车系列答案
阅读快车系列答案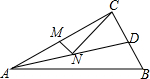 如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=3cm,AD平分∠CAB交BC于点D,点M,N分别是AC和AD边上的动点,则MN+NC的最小值为( )
如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=3cm,AD平分∠CAB交BC于点D,点M,N分别是AC和AD边上的动点,则MN+NC的最小值为( )| A. | $\frac{3}{2}$ | B. | 2 | C. | $\frac{5}{2}$ | D. | $\frac{12}{5}$ |
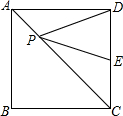 正方形ABCD中,点P是对角线AC上的动点,点E是CD的中点,AB=2,求PD+PE的最小值.
正方形ABCD中,点P是对角线AC上的动点,点E是CD的中点,AB=2,求PD+PE的最小值. 如图是一个三角形数阵,根据该数阵的规律,猜想第八行所有数的和是512.
如图是一个三角形数阵,根据该数阵的规律,猜想第八行所有数的和是512.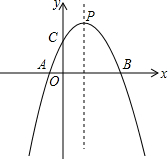 如图,抛物线y=-x2+bx+c的对称轴是直线x=1,与y轴交于点C(0,3),与x轴交于 A,B两点.
如图,抛物线y=-x2+bx+c的对称轴是直线x=1,与y轴交于点C(0,3),与x轴交于 A,B两点.