题目内容
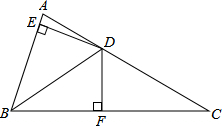 如图,在△ABC中,∠ABC=2∠C,BD平分∠ABC,DE⊥AB(E在AB之间),DF⊥BC,已知BD=5,DE=3,CF=4,试求△DFC的周长.
如图,在△ABC中,∠ABC=2∠C,BD平分∠ABC,DE⊥AB(E在AB之间),DF⊥BC,已知BD=5,DE=3,CF=4,试求△DFC的周长.考点:角平分线的性质
专题:
分析:根据角平分线的性质可证∠ABD=∠CBD,即可求得∠CBD=∠C,即BD=CD,再根据角平分线上的点到角两边距离相等即可求得DE=DF,即可解题.
解答:解:∵∠ABC=2∠C,BD平分∠ABC,
∴∠CBD=∠C,
∴BD=CD,
∵BD平分∠ABC,
∴DE=DF,
∴△DFC的周长=DF+CD+CF=DE+BD+CF=3+5+4=12.
∴∠CBD=∠C,
∴BD=CD,
∵BD平分∠ABC,
∴DE=DF,
∴△DFC的周长=DF+CD+CF=DE+BD+CF=3+5+4=12.
点评:本题考查了角平分线上点到角两边距离相等的性质,考查了角平分线平分角的性质,考查了三角形周长的计算,本题中求证DE=DF是解题的关键.

练习册系列答案
相关题目
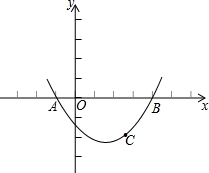 如图,已知抛物线过点A(-1,0),B(4,0),C(
如图,已知抛物线过点A(-1,0),B(4,0),C(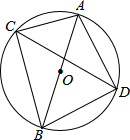 已知A、B、C三点位于⊙O上,其中AB连线过圆心,DC是∠ACB的角平分线,D点也在⊙O上,已知AC=6,AB=10,求BC、AD、BD的长.
已知A、B、C三点位于⊙O上,其中AB连线过圆心,DC是∠ACB的角平分线,D点也在⊙O上,已知AC=6,AB=10,求BC、AD、BD的长. 已知正方形ABCD的边长是2,点E、F分别是BC、CD的中点,AE与BF交于点O.
已知正方形ABCD的边长是2,点E、F分别是BC、CD的中点,AE与BF交于点O. 如图,锐角三角形ABC的两条高BE、CD相交于点O,且OB=OC
如图,锐角三角形ABC的两条高BE、CD相交于点O,且OB=OC 几何体简称为体,按其形状可分为三类,即柱体、椎体、球体,下列图形中:
几何体简称为体,按其形状可分为三类,即柱体、椎体、球体,下列图形中: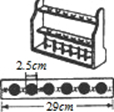 如图是学校化学实验室用于放试管的木架,在每层长29cm的木条上钻有6个圆孔,每个圆孔的直径均为2.5cm.两端与圆孔边缘及任何相邻两孔边缘之间的距离都相等并设为xcm,则x为
如图是学校化学实验室用于放试管的木架,在每层长29cm的木条上钻有6个圆孔,每个圆孔的直径均为2.5cm.两端与圆孔边缘及任何相邻两孔边缘之间的距离都相等并设为xcm,则x为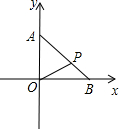 如图,点B,A分别在x,y轴的正半轴上,AB=m,且AP:PB=2:1,点B在x轴的正半轴上移动,线段AB的长保持不变.
如图,点B,A分别在x,y轴的正半轴上,AB=m,且AP:PB=2:1,点B在x轴的正半轴上移动,线段AB的长保持不变.