题目内容
14.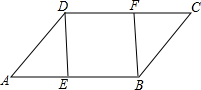 如图,在?ABCD中,E、F分别是AB、DC边上的点,且AE=CF,
如图,在?ABCD中,E、F分别是AB、DC边上的点,且AE=CF,(1)求证:△ADE≌△CBF.
(2)若∠DEB=90°,求证:四边形DEBF是矩形.
分析 (1)由在?ABCD中,AE=CF,可利用SAS判定△ADE≌△CBF.
(2)由在?ABCD中,且AE=CF,利用一组对边平行且相等的四边形是平行四边形,可证得四边形DEBF是平行四边形,又由∠DEB=90°,可证得四边形DEBF是矩形.
解答 证明:(1)∵四边形ABCD是平行四边形,
∴AD=CB,∠A=∠C,
在△ADE和△CBF中,
$\left\{\begin{array}{l}{AD=CB}\\{∠A=∠C}\\{AE=CF}\end{array}\right.$,
∴△ADE≌△CBF(SAS).
(2)∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∵AE=CF,
∴BE=DF,
∴四边形DEBF是平行四边形,
∵∠DEB=90°,
∴四边形DEBF是矩形.
点评 此题考查了平行四边形的判定与性质、矩形的判定以及全等三角形的判定与性质.注意有一个角是直角的平行四边形是矩形,首先证得四边形ABCD是平行四边形是关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
4.实数-$\frac{1}{2}$的相反数是( )
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | 2 | D. | -2 |
2. 如图,在△ABC中,AB=AD=DC,∠B=70°,则∠C的度数为( )
如图,在△ABC中,AB=AD=DC,∠B=70°,则∠C的度数为( )
 如图,在△ABC中,AB=AD=DC,∠B=70°,则∠C的度数为( )
如图,在△ABC中,AB=AD=DC,∠B=70°,则∠C的度数为( )| A. | 35° | B. | 40° | C. | 45° | D. | 50° |
9.不等式组$\left\{\begin{array}{l}{x+4>3}\\{2x≤4}\end{array}\right.$的解集是( )
| A. | 1<x≤2 | B. | -1<x≤2 | C. | x>-1 | D. | -1<x≤4 |
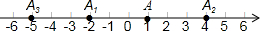 如图,在数轴上,点A表示1,现将点A沿x轴做如下移动,第一次点A向左移动3个单位长度到达点A1,第二次将点A1向右移动6个单位长度到达点A2,第三次将点A2向左移动9个单位长度到达点A3,按照这种移动规律移动下去,第n次移动到点An,如果点An与原点的距离不小于20,那么n的最小值是13.
如图,在数轴上,点A表示1,现将点A沿x轴做如下移动,第一次点A向左移动3个单位长度到达点A1,第二次将点A1向右移动6个单位长度到达点A2,第三次将点A2向左移动9个单位长度到达点A3,按照这种移动规律移动下去,第n次移动到点An,如果点An与原点的距离不小于20,那么n的最小值是13.
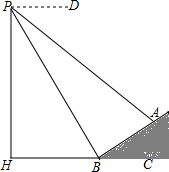 如图,数学实习小组在高500米的山腰(即PH=500米)P处进行测量,测得对面山坡上,A处的仰角为30°,对面山脚B处的俯角60°.已知tan∠ABC=$\frac{\sqrt{3}}{3}$,点P,H,B,C,A在同一个平面上,点H,B,C在同一条直线上,且PH⊥HC.
如图,数学实习小组在高500米的山腰(即PH=500米)P处进行测量,测得对面山坡上,A处的仰角为30°,对面山脚B处的俯角60°.已知tan∠ABC=$\frac{\sqrt{3}}{3}$,点P,H,B,C,A在同一个平面上,点H,B,C在同一条直线上,且PH⊥HC. 如图,已知在矩形ABCD中,点E在边BC上,BE=2CE,将矩形沿着过点E的直线翻折后,点C、D分别落在边BC下方的点C′、D′处,且点C′、D′、B在同一条直线上,折痕与边AD交于点F,D′F与BE交于点G.设AB=2$\sqrt{3}$,那么△EFG的周长为12.
如图,已知在矩形ABCD中,点E在边BC上,BE=2CE,将矩形沿着过点E的直线翻折后,点C、D分别落在边BC下方的点C′、D′处,且点C′、D′、B在同一条直线上,折痕与边AD交于点F,D′F与BE交于点G.设AB=2$\sqrt{3}$,那么△EFG的周长为12.