题目内容
2. 如图,在△ABC中,AB=AD=DC,∠B=70°,则∠C的度数为( )
如图,在△ABC中,AB=AD=DC,∠B=70°,则∠C的度数为( )| A. | 35° | B. | 40° | C. | 45° | D. | 50° |
分析 先根据等腰三角形的性质求出∠ADB的度数,再由平角的定义得出∠ADC的度数,根据等腰三角形的性质即可得出结论.
解答 解:∵△ABD中,AB=AD,∠B=70°,
∴∠B=∠ADB=70°,
∴∠ADC=180°-∠ADB=110°,
∵AD=CD,
∴∠C=(180°-∠ADC)÷2=(180°-110°)÷2=35°,
故选:A.
点评 本题考查的是等腰三角形的性质,熟知等腰三角形的两底角相等是解答此题的关键.

练习册系列答案
相关题目
13.下列图形中,是轴对称图形,但不是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
16.一个物体从A点出发,沿坡度为1:7的斜坡向上直线运动到B,AB=30米时,物体升高( )米.
| A. | $\frac{30}{7}$ | B. | 3$\sqrt{2}$ | ||
| C. | $\frac{30}{6}$ | D. | 以上的答案都不对 |
 .
. 如图是由四个大小相同的正方体组成的几何体,那么它的主视图是( )
如图是由四个大小相同的正方体组成的几何体,那么它的主视图是( )



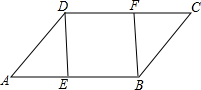 如图,在?ABCD中,E、F分别是AB、DC边上的点,且AE=CF,
如图,在?ABCD中,E、F分别是AB、DC边上的点,且AE=CF,



