Question

11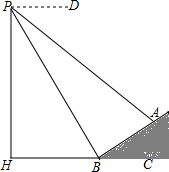．如图，数学实习小组在高500米的山腰（即PH=500米）P处进行测量，测得对面山坡上，A处的仰角为30°，对面山脚B处的俯角60°．已知tan∠ABC=$\frac{\sqrt{3}}{3}$，点P，H，B，C，A在同一个平面上，点H，B，C在同一条直线上，且PH⊥HC．
（1）求∠ABP的度数；
（2）求A，B两点间的距离．

Answer 1

分析 （1）根据俯角以及坡度的定义即可求解；
（2）在直角△PHB中，根据三角函数即可求得PB的长，然后在直角△PBA中利用三角函数即可求解．

解答 解：（1）∵tan∠ABC=$\frac{\sqrt{3}}{3}$，
∴∠ABC=30°；
∵从P点望山脚B处的俯角60°，
∴∠PBH=60°，
∴∠ABP=180°-30°-60°=90°

（2）由题意得：∠PBH=60°，
∵∠ABC=30°，
∴∠ABP=90°
∴△PAB为直角三角形，
在直角△PHB中，PB=PH÷sin∠PBH=$\frac{1000\sqrt{3}}{3}$（m）．
在直角△PBA中，AB=PB•tan∠BPA=$\frac{1000}{3}$（m）．
∴A、B两点之间的距离为$\frac{1000}{3}$米．

点评 本题主要考查了俯角的问题以及坡度的定义，正确利用三角函数的定义是解题的关键．