题目内容
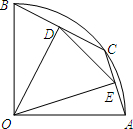 如图,在半径为2的扇形OAB,∠AOB=90°,点C是
如图,在半径为2的扇形OAB,∠AOB=90°,点C是 |
| AB |
| A、1 | ||
| B、2 | ||
C、
| ||
D、
|
考点:垂径定理,三角形中位线定理
专题:
分析:连接AB,由OD垂直于BC,OE垂直于AC,利用垂径定理得到D、E分别为BC、AC的中点,即ED为三角形ABC的中位线,由OA=OB=2,且∠AOB=90°,利用勾股定理求出AB的长,即可求出DE的长.
解答: 解:连接AB,
解:连接AB,
∵OD⊥BC,OE⊥AC,
∴D、E分别为BC、AC的中点,
∴DE为△ABC的中位线,
∵OA=OB=2,∠AOB=90°,
∴根据勾股定理得:AB=
=2
,
∴DE=
AB=
.
故选C.
 解:连接AB,
解:连接AB,∵OD⊥BC,OE⊥AC,
∴D、E分别为BC、AC的中点,
∴DE为△ABC的中位线,
∵OA=OB=2,∠AOB=90°,
∴根据勾股定理得:AB=
| OA2+OB2 |
| 2 |
∴DE=
| 1 |
| 2 |
| 2 |
故选C.
点评:此题考查了垂径定理,勾股定理,以及三角形的中位线定理,熟练掌握定理是解本题的关键.

练习册系列答案
 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
下列等式的变形错误的是( )
| A、由a=b得a+5=b+5 | ||||
B、由a=b得
| ||||
| C、由x+2=y+2得x=y | ||||
| D、由-3x=-3y得x=-y |
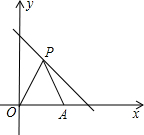 如图,在平面直角坐标系中,点P(x,y)是第一象限直线y=-x+6的点,点A(4,0),O是坐标原点,△PAO的面积为S.
如图,在平面直角坐标系中,点P(x,y)是第一象限直线y=-x+6的点,点A(4,0),O是坐标原点,△PAO的面积为S. 给窗户装遮阳棚,其目的为最大限度地遮挡夏天炎热的阳光,又能最大限度地使冬天温暖的阳光射入室内,现请你为我校新建成的高中部教学楼朝南的窗户设计一个直角形遮阳蓬BCD,如图,已知窗户AB高度为h=2米,本地冬至日正午时刻太阳光与地面的最小夹角α=32°,夏至日正午时刻太阳光与地面的最大夹角β=79°,请分别计算直角形遮阳蓬BCD中BC、CD的长(结果精确到0.1米)
给窗户装遮阳棚,其目的为最大限度地遮挡夏天炎热的阳光,又能最大限度地使冬天温暖的阳光射入室内,现请你为我校新建成的高中部教学楼朝南的窗户设计一个直角形遮阳蓬BCD,如图,已知窗户AB高度为h=2米,本地冬至日正午时刻太阳光与地面的最小夹角α=32°,夏至日正午时刻太阳光与地面的最大夹角β=79°,请分别计算直角形遮阳蓬BCD中BC、CD的长(结果精确到0.1米) 如图,
如图,