题目内容
用平方差公式进行计算:
(1-
)(1-
)(1-
)…(1-
).
(1-
| 1 |
| 22 |
| 1 |
| 32 |
| 1 |
| 42 |
| 1 |
| 20132 |
考点:平方差公式
专题:计算题
分析:原式括号中两项利用平方差公式变形,计算即可得到结果.
解答:解:原式=(1+
)(1-
)(1+
)(1-
)…(1+
)(1-
)
=
×
×
×
×
×
…×
×
=
.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2013 |
| 1 |
| 2013 |
=
| 1 |
| 2 |
| 3 |
| 2 |
| 2 |
| 3 |
| 4 |
| 3 |
| 3 |
| 4 |
| 5 |
| 4 |
| 2012 |
| 2013 |
| 2014 |
| 2013 |
=
| 1012 |
| 2013 |
点评:此题考查了平方差公式,熟练掌握平方差公式是解本题的关键.

练习册系列答案
相关题目
在3,-1,0,-2这四个数中,最小的数是( )
| A、0 | B、-1 | C、-2 | D、3 |
已知a-b=-10,c+d=5,则(b+c)-(a-d)为( )
| A、10 | B、15 | C、5 | D、-5 |
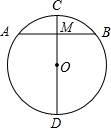 如图,在⊙O中,CD是直径,AB是弦,且CD⊥AB,已知AB=8,CM=2,求直径CD的长.
如图,在⊙O中,CD是直径,AB是弦,且CD⊥AB,已知AB=8,CM=2,求直径CD的长.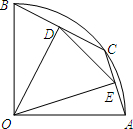 如图,在半径为2的扇形OAB,∠AOB=90°,点C是
如图,在半径为2的扇形OAB,∠AOB=90°,点C是
 如图,AB∥CD,MG平分∠BMN,NH平分∠MND,且MG与NH相交于点O,证明:MG⊥NH.
如图,AB∥CD,MG平分∠BMN,NH平分∠MND,且MG与NH相交于点O,证明:MG⊥NH.