题目内容
观察下列各等式,
=
-
,
=
-
,
=
-
…,根据你发现的规律,计算
+
+
+…+
= (n为正整数)
| 1 |
| 1×2 |
| 1 |
| 1 |
| 1 |
| 2 |
| 1 |
| 2×3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3×4 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| n(n+1) |
考点:分式的加减法
专题:规律型
分析:根据题意归纳总结得到拆项规律,原式利用拆项法变形后,计算即可得到结果.
解答:解:原式=1-
+
-
+…+
-
=1-
=
,
故答案为:
.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| n+1 |
=1-
| 1 |
| n+1 |
=
| n |
| n+1 |
故答案为:
| n |
| n+1 |
点评:此题考查了分式的加减法,弄清拆项规律是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知x=3是关于x的方程ax+2x-3=0的解,则a的值为( )
| A、-1 | B、-2 | C、-3 | D、1 |
下列命题是真命题的是( )
| A、等腰梯形的对角线相等 |
| B、一组对边平行且另一组对边相等的四边形是平行四边形 |
| C、矩形的对角线互相垂直 |
| D、对角线互相垂直且相等的四边形是正方形 |
下列格式由左边到右边的变形中,属于分解因式的是( )
| A、2(x+y)=2x+2y |
| B、x2-4x+4=x(x-4)+4 |
| C、10x2-5x=5x(2x-1) |
| D、x2-16+6x=(x+4)(x-4)+6x |
 如图,在△ABC中,AB=12,AC=18,AD是∠BAC的平分线,过点B作AD的垂线,交AD于D,M是BC的中点,求MD的长.
如图,在△ABC中,AB=12,AC=18,AD是∠BAC的平分线,过点B作AD的垂线,交AD于D,M是BC的中点,求MD的长.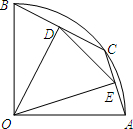 如图,在半径为2的扇形OAB,∠AOB=90°,点C是
如图,在半径为2的扇形OAB,∠AOB=90°,点C是
 如图,AB∥CD,MG平分∠BMN,NH平分∠MND,且MG与NH相交于点O,证明:MG⊥NH.
如图,AB∥CD,MG平分∠BMN,NH平分∠MND,且MG与NH相交于点O,证明:MG⊥NH.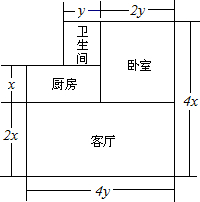 如图是小明家的住房结构平面图(单位:米),他打算把卧室以外的部分都铺上地砖.
如图是小明家的住房结构平面图(单位:米),他打算把卧室以外的部分都铺上地砖. 一木杆在离地面3m处折断,木杆顶端落在离木杆底端4m处,木杆折断以前有多少米?
一木杆在离地面3m处折断,木杆顶端落在离木杆底端4m处,木杆折断以前有多少米?