题目内容
 如图,
如图, |
| AB |
 |
| AB |
考点:弧长的计算
专题:
分析:连接AO、CO,首先求得弦心距CO是60-30=30,则在直角三角形中,根据锐角三角函数,可以求得∠AOB=60°×2=120°.再根据弧长公式即可计算.
解答:解:连接AO、CO,
则CO=R-h=60-30=30,
在△BCO中,
∵cos∠COB=
=
=
,
∴∠COB=60°,
∴∠AOB=60°×2=120°,
则
=
=40π.
故答案为:40π.
则CO=R-h=60-30=30,

在△BCO中,
∵cos∠COB=
| OC |
| OB |
| 30 |
| 60 |
| 1 |
| 2 |
∴∠COB=60°,
∴∠AOB=60°×2=120°,
则
 |
| AB |
| 120π×60 |
| 180 |
故答案为:40π.
点评:本题考查了弧长公式,首先要根据边之间的关系求得其弧所对的圆心角的度数,再进一步根据弧长公式计算.

练习册系列答案
相关题目
点P(x,y)在第四象限,P到x轴,y轴的距离分别等于5和3,则P点的坐标是( )
| A、(-3,-5) |
| B、(5,-3) |
| C、(3,-5) |
| D、(-3,5)2 |
在3,-1,0,-2这四个数中,最小的数是( )
| A、0 | B、-1 | C、-2 | D、3 |
已知a-b=-10,c+d=5,则(b+c)-(a-d)为( )
| A、10 | B、15 | C、5 | D、-5 |
若关于x的方程2x+a-4=0的解是x=-2,则a的值等于( )
| A、-8 | B、0 | C、2 | D、8 |
下列各运算中,正确的是( )
| A、a2•a3=a6 |
| B、(-3a3)2=9a6 |
| C、a4+a2=a6 |
| D、(a+2)2=a2+4 |
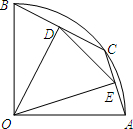 如图,在半径为2的扇形OAB,∠AOB=90°,点C是
如图,在半径为2的扇形OAB,∠AOB=90°,点C是 如图,AB∥CD,MG平分∠BMN,NH平分∠MND,且MG与NH相交于点O,证明:MG⊥NH.
如图,AB∥CD,MG平分∠BMN,NH平分∠MND,且MG与NH相交于点O,证明:MG⊥NH.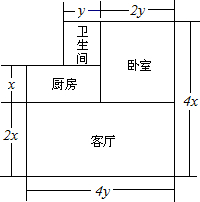 如图是小明家的住房结构平面图(单位:米),他打算把卧室以外的部分都铺上地砖.
如图是小明家的住房结构平面图(单位:米),他打算把卧室以外的部分都铺上地砖.