题目内容
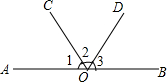 如图,射线OC、OD将平角AOB平分成大小不等的三个角∠1、∠2、∠3.
如图,射线OC、OD将平角AOB平分成大小不等的三个角∠1、∠2、∠3.(1)若∠1-∠2=∠2-∠3,则∠2的度数是否可求?如可求,算出该度数?若不能,请说明理由?
(2)在(1)的条件下,又知∠1=2∠3,试求∠3的度数?
考点:角的计算
专题:
分析:(1)由∠1-∠2=∠2-∠3,可得:2∠2=∠1+∠3,然后由∠1+∠2+∠3=180°,可求∠2的度数;
(2)由(1)求出∠2的度数,然后根据2∠2=∠1+∠3,∠1=2∠3.即可求出∠3的度数.
(2)由(1)求出∠2的度数,然后根据2∠2=∠1+∠3,∠1=2∠3.即可求出∠3的度数.
解答:解:(1)∵∠1-∠2=∠2-∠3,
∴2∠2=∠1+∠3,
∵∠1+∠2+∠3=180°,
∴3∠2=180°,
∴∠2=60°.
(2)∵2∠2=∠1+∠3,∠2=60°,
∴∠1+∠3=120°,
∵∠1=2∠3,
∴3∠3=120°,
∴∠3=40°.
∴2∠2=∠1+∠3,
∵∠1+∠2+∠3=180°,
∴3∠2=180°,
∴∠2=60°.
(2)∵2∠2=∠1+∠3,∠2=60°,
∴∠1+∠3=120°,
∵∠1=2∠3,
∴3∠3=120°,
∴∠3=40°.
点评:此题考查了角的计算,解题的关键是:利用1平角=180°解决问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
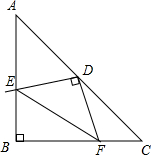 如图,在等腰△ABC中,∠ABC=90°,将直角三角板的直角顶点与AC的中点重合,把三角板绕着点D旋转,两条直角边分别交边AB于E,交边BC于F,若AB=
如图,在等腰△ABC中,∠ABC=90°,将直角三角板的直角顶点与AC的中点重合,把三角板绕着点D旋转,两条直角边分别交边AB于E,交边BC于F,若AB=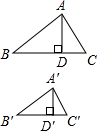 如图,△ABC∽△A′B′C′,AD、A′D′分别是它们的高,求证:
如图,△ABC∽△A′B′C′,AD、A′D′分别是它们的高,求证: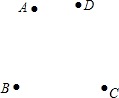 如图,学校有四幢教学楼,四幢教学楼之间是一个大操场,学校打算在操场上安置一组健身器材,使每幢教学楼的学生到健身器材处的距离和最小,请在图中画出健身器材的安置点P.
如图,学校有四幢教学楼,四幢教学楼之间是一个大操场,学校打算在操场上安置一组健身器材,使每幢教学楼的学生到健身器材处的距离和最小,请在图中画出健身器材的安置点P. 如图,线段AB=8cm.
如图,线段AB=8cm.