题目内容
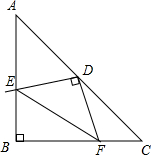 如图,在等腰△ABC中,∠ABC=90°,将直角三角板的直角顶点与AC的中点重合,把三角板绕着点D旋转,两条直角边分别交边AB于E,交边BC于F,若AB=
如图,在等腰△ABC中,∠ABC=90°,将直角三角板的直角顶点与AC的中点重合,把三角板绕着点D旋转,两条直角边分别交边AB于E,交边BC于F,若AB=| 5 |
考点:全等三角形的判定与性质,等腰直角三角形
专题:
分析:连接BD,根据等腰三角形的性质和直角三角形斜边上中线性质得出AD=DC=BD,∠A=∠C=45°,∠ABD=∠CBD=45°,BD⊥AC,求出∠ADB=∠CDB=90°,∠EDB=∠FDC,证出△EDB≌△FDC,推出S△EDB=S△FDC,同理S△ADE=S△BDF,求出△ABC的面积即可.
解答:解:连接BD,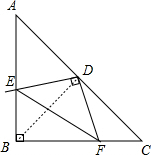
∵△ABC是等腰直角三角形,D为斜边AC的中点,
∴AD=DC=BD,∠A=∠C=45°,∠ABD=∠CBD=45°,BD⊥AC,
∴∠ADB=∠CDB=90°,
∵∠EDF=90°,
∴∠EDB=∠FDC=90°-∠BDF,
在△EDB和△FDC中,
,
∴△EDB≌△FDC(ASA),
∴S△EDB=S△FDC,
同理S△ADE=S△BDF,
∵AB=
,
∴BC=AB=
,
∴S△ABC=
×AB×BC=
×
×
=
,
∴S△ADE+S△DFC=
S△ABC=
×
=
,
故答案为:
.

∵△ABC是等腰直角三角形,D为斜边AC的中点,
∴AD=DC=BD,∠A=∠C=45°,∠ABD=∠CBD=45°,BD⊥AC,
∴∠ADB=∠CDB=90°,
∵∠EDF=90°,
∴∠EDB=∠FDC=90°-∠BDF,
在△EDB和△FDC中,
|
∴△EDB≌△FDC(ASA),
∴S△EDB=S△FDC,
同理S△ADE=S△BDF,
∵AB=
| 5 |
∴BC=AB=
| 5 |
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 5 |
| 5 |
| 2 |
∴S△ADE+S△DFC=
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
| 5 |
| 4 |
故答案为:
| 5 |
| 4 |
点评:本题考查了全等三角形的性质和判定,等腰三角形的性质,直角三角形斜边上的中线性质的应用,解此题的关键是推出△EDB≌△FDC和△ADE≌△BDF.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
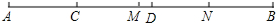 如图,已知C、D两点将线段AB分为三部分,且AC:CD:DB=2:3:4,若AB的中点为M,BD的中点为N,且MN=5cm,求AB的长.
如图,已知C、D两点将线段AB分为三部分,且AC:CD:DB=2:3:4,若AB的中点为M,BD的中点为N,且MN=5cm,求AB的长.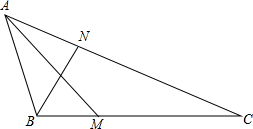 如图,在△ABC中,∠BAC=40°,∠ABC=120°,AM、BN分别为∠BAC,∠ABC的角平分线,证明:AB+AN=AM+BM.
如图,在△ABC中,∠BAC=40°,∠ABC=120°,AM、BN分别为∠BAC,∠ABC的角平分线,证明:AB+AN=AM+BM.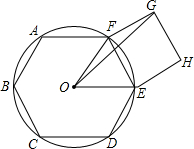 如图,半径为R的圆内,ABCDEF是正六边形,EFGH是正方形.
如图,半径为R的圆内,ABCDEF是正六边形,EFGH是正方形.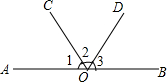 如图,射线OC、OD将平角AOB平分成大小不等的三个角∠1、∠2、∠3.
如图,射线OC、OD将平角AOB平分成大小不等的三个角∠1、∠2、∠3. 如图,在平面直角坐标系xOy中,直线AB与x轴交于点A,与y轴交于点C(0,2),且与反比例函数
如图,在平面直角坐标系xOy中,直线AB与x轴交于点A,与y轴交于点C(0,2),且与反比例函数