题目内容
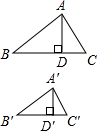如图，△ABC∽△A′B′C′，AD、A′D′分别是它们的高，求证：| AD |
| A′D′ |
| BC |
| B′C′ |
考点：相似三角形的判定与性质
专题：证明题
分析：由△ABC∽△A′B′C′可得∠B=∠B′，可证得△ABD∽△A′B′D′，可得
=
，且
=
，可得结论．
| AD |
| A′D′ |
| AB |
| A′B′ |
| AB |
| A′B′ |
| BC |
| B′C′ |
解答：证明：
∵△ABC∽△A′B′C′，
∴∠B=∠B′，
=
，
又∵AD⊥BC，A′D′⊥B′C′，
∴∠ADB=∠A′D′B′，
∴△ABD∽△A′B′D′，
∴
=
，
∴
=
．
∵△ABC∽△A′B′C′，
∴∠B=∠B′，
| AB |
| A′B′ |
| BC |
| B′C′ |
又∵AD⊥BC，A′D′⊥B′C′，
∴∠ADB=∠A′D′B′，
∴△ABD∽△A′B′D′，
∴
| AD |
| A′D′ |
| AB |
| A′B′ |
∴
| AD |
| A′D′ |
| BC |
| B′C′ |
点评：本题主要考查相似三角形的判定和性质，掌握相似三角形的对应角相等，对应边成比例是解题的关键．
练习册系列答案
相关题目
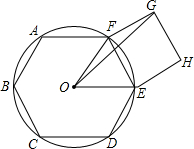如图，半径为R的圆内，ABCDEF是正六边形，EFGH是正方形．
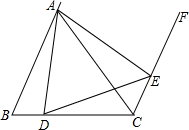已知等边△ABC，AB∥CF，点D在BC上，E在CF上，∠ADE=60°，问△ADE是等边三角形吗？
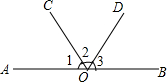如图，射线OC、OD将平角AOB平分成大小不等的三个角∠1、∠2、∠3．
如图，BD、CE是△ABC的两条高，连接DE．
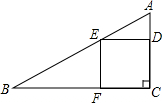在Rt△ABC中，∠C=90°，AC=6，BC=12，在AC上有一动点D（不与A、C重合），作DE∥BC交AB于点E，作EF∥AC交BC于点F．当点D在什么位置时，四边形CDEF的面积最大？
如图，⊙O为△ABC的内切圆，∠C=90°，AO的延长线交BC于点D，AC=4，CD=2，求⊙O的半径．