题目内容
 如图,线段AB=8cm.
如图,线段AB=8cm.(1)若C是线段AB上一点,M是AC的中点,N是BC的中点,求线段MN的长;
(2)若将第(1)题中点C的位置改为“C是线段AB的延长线上的任意一点”,你能求出线段MN的长吗?
解:(1)因为M是AC的中点,N是BC的中点,
所以MC=
因为MN=MC+NC,
所以MN=
=
=4(cm).
请仿照上面的表述完成第(2)题,并画出图形.
考点:两点间的距离
专题:
分析:(1)根据M是AC的中点,N是BC的中点得出MC=
AC,NC=
BC,再根据MN=MC+NC即可得出结论;
(2)根据题意画出图形,根据(1)中的过程即可得出结论.
| 1 |
| 2 |
| 1 |
| 2 |
(2)根据题意画出图形,根据(1)中的过程即可得出结论.
解答:解:(1)∵M是AC的中点,N是BC的中点,
∴MC=
AC,NC=
BC,
∴MN=MC+NC=
(AC+BC)=
AB=4cm.
故答案为:
,
,
AC,
BC,
AB;
(2)如图所示,
∵M是AC的中点,N是BC的中点,
∴MC=
AC=
(AB+BC),BN=
BC,
∴MN=MC-NC=
(AB+BC-BC)=
AB=4cm.
∴MC=
| 1 |
| 2 |
| 1 |
| 2 |
∴MN=MC+NC=
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(2)如图所示,
∵M是AC的中点,N是BC的中点,

∴MC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴MN=MC-NC=
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查的是两点间的距离,熟知各线段之间的和、差及倍数关系是解答此题的关键.

练习册系列答案
相关题目
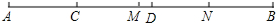 如图,已知C、D两点将线段AB分为三部分,且AC:CD:DB=2:3:4,若AB的中点为M,BD的中点为N,且MN=5cm,求AB的长.
如图,已知C、D两点将线段AB分为三部分,且AC:CD:DB=2:3:4,若AB的中点为M,BD的中点为N,且MN=5cm,求AB的长.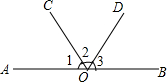 如图,射线OC、OD将平角AOB平分成大小不等的三个角∠1、∠2、∠3.
如图,射线OC、OD将平角AOB平分成大小不等的三个角∠1、∠2、∠3.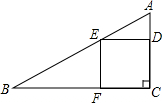 在Rt△ABC中,∠C=90°,AC=6,BC=12,在AC上有一动点D(不与A、C重合),作DE∥BC交AB于点E,作EF∥AC交BC于点F.当点D在什么位置时,四边形CDEF的面积最大?
在Rt△ABC中,∠C=90°,AC=6,BC=12,在AC上有一动点D(不与A、C重合),作DE∥BC交AB于点E,作EF∥AC交BC于点F.当点D在什么位置时,四边形CDEF的面积最大? 如图,⊙O为△ABC的内切圆,∠C=90°,AO的延长线交BC于点D,AC=4,CD=2,求⊙O的半径.
如图,⊙O为△ABC的内切圆,∠C=90°,AO的延长线交BC于点D,AC=4,CD=2,求⊙O的半径. 如图,在平面直角坐标系xOy中,直线AB与x轴交于点A,与y轴交于点C(0,2),且与反比例函数
如图,在平面直角坐标系xOy中,直线AB与x轴交于点A,与y轴交于点C(0,2),且与反比例函数 如图,已知二次函数y=ax2+bx+c(a≠0)的图象,则a+b+c
如图,已知二次函数y=ax2+bx+c(a≠0)的图象,则a+b+c 如图,AB是⊙O的直径,C是⊙O上一点(不与A、B重合),D是劣弧
如图,AB是⊙O的直径,C是⊙O上一点(不与A、B重合),D是劣弧