题目内容
19．一名跳水运动员从距水面10米高的跳台向上跳起0.8米，最后以12米/秒的向下运动速度入水，他在空中每完成一个翻滚动作需用时0.4秒，并至少在离水面2米处停止做翻滚动作准备入水，该运动员在空中至多能做（ ）个翻滚动作．| A． | 3 | B． | 4 | C． | 5 | D． | 6 |
分析 因为从10米高的跳起0.8米，可以看成是从10.8米高的地方自由落体 所以入水t=$\frac{{v}_{t}-{v}_{0}}{g}$，t=12÷9.8=1.22秒还要加上开始的0.8米：减速上抛运动S=$\frac{1}{2}$gt2 计算出t为0.40s，所以总时间是1.22+0.4=1.62，由此除以翻滚动作需用时0.4秒得出答案即可．
解答 解：∵t=$\frac{{v}_{t}-{v}_{0}}{g}$，
t=12÷9.8=1.22s，
速上抛运动S=$\frac{1}{2}$gt2，
t=$\sqrt{\frac{0.8×2}{9.8}}$=0.40s，
∴总时间：1.22+0.4=1.62s，
∴翻滚动作最多：1.62÷0.4=4（个）
故选：B．
点评 此题考查一元二次方程的实际运用，掌握落体运动物体的运动速度与时间的关系是解决问题的关键．
练习册系列答案
名校课堂系列答案
相关题目
已知y=ax2+bx+c的图象如下，则：a+b+c＜0，a-b+c＞0，2a-b=0．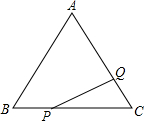
如图，等边三角形ABC的边长为6cm，点P自点B出发，以1cm/s的速度向终点C运动；点Q自点C出发，以1cm/s的速度向终点A运动．若P，Q两点分别同时从B，C两点出发，问经过多少时间△PCQ的面积是2$\sqrt{3}$cm2？
有理数a和b在数轴上的位置如图所示，下列五个结论：
8．关于函数y=-$\frac{1}{2}$x，下列结论正确的是（ ）
| A． | 函数图象必过点（-2，-1） | B． | 函数图象经过第1、3象限 | ||
| C． | y随x的增大而减小 | D． | y随x的增大而增大 |