题目内容
20.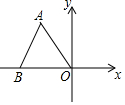 等边△ABO在平面直角坐标系内的位置如图所示,已知△ABO的边长为6,则点A的坐标为( )
等边△ABO在平面直角坐标系内的位置如图所示,已知△ABO的边长为6,则点A的坐标为( )| A. | (-3,3) | B. | (3,-3$\sqrt{3}$) | C. | (-3,3$\sqrt{3}$) | D. | (-3,-3$\sqrt{3}$) |
分析 过点A作AC⊥x轴于点C,然后根据三线合一即可求出AC和OC的长度.
解答 解: 过点A作AC⊥x轴于点C,
过点A作AC⊥x轴于点C,
∵∠AOB=60°
∴∠CAO=30°,
∴CO=$\frac{1}{2}$AO=3,
∴由勾股定理可知:AC=3$\sqrt{3}$,
∴A(-3,3$\sqrt{3}$),
故选(C)
点评 本题考查等边三角形的性质,解题的关键是根据等边三角形的性质求出OC与AC的长度,本题属于基础题型.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8.在一个不透明的口袋里装有颜色不同的红、白两种颜色的球共5只,某学习小组做摸球实验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复,下表是活动进行中的一组统计数据:
(1)请估计:当n很大时,摸到白球的频率将会接近0.6;(精确到0.1)
(2)试估算口袋中白球有多少只?
(3)请画树状图或列表计算:从中先摸出一球,不放回,再摸出一球;这两只球颜色不同的概率是多少?
| 摸球的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
| 摸到白球的次数m | 58 | 96 | 116 | 295 | 484 | 601 |
| 摸到白球的频率 | 0.58 | 0.64 | 0.58 | 0.59 | 0.605 | 0.601 |
(2)试估算口袋中白球有多少只?
(3)请画树状图或列表计算:从中先摸出一球,不放回,再摸出一球;这两只球颜色不同的概率是多少?
12.下列说法中,正确的是( )
| A. | 0是整数 | B. | 3.14不是分数 | ||
| C. | -(+1)<+(-2) | D. | 倒数等于其本身的数有1,-1,0 |
9.已知三角形两边的长分别是6和12,则此三角形第三边的长可能是( )
| A. | 5 | B. | 6 | C. | 11 | D. | 18 |
10. 如图,⊙O的半径为4,△ABC是⊙O的内接三角形,连接OB、OC,若∠BAC与∠BOC互补,则弦BC的长为( )
如图,⊙O的半径为4,△ABC是⊙O的内接三角形,连接OB、OC,若∠BAC与∠BOC互补,则弦BC的长为( )
 如图,⊙O的半径为4,△ABC是⊙O的内接三角形,连接OB、OC,若∠BAC与∠BOC互补,则弦BC的长为( )
如图,⊙O的半径为4,△ABC是⊙O的内接三角形,连接OB、OC,若∠BAC与∠BOC互补,则弦BC的长为( )| A. | 7$\sqrt{3}$ | B. | 6$\sqrt{3}$ | C. | 5$\sqrt{3}$ | D. | 4$\sqrt{3}$ |
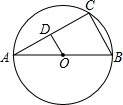 如图,AB为⊙O的直径,点C是⊙O上的一点,AB=8cm,∠A=30°,点D是弦AC上的一点,动点P从点C沿CA以2cm/s的速度向点D运动,再沿DO以1cm/s的速度向点O运动,设点P在整个运动过程中的时间为t,则t的最小值是2$\sqrt{3}$s.
如图,AB为⊙O的直径,点C是⊙O上的一点,AB=8cm,∠A=30°,点D是弦AC上的一点,动点P从点C沿CA以2cm/s的速度向点D运动,再沿DO以1cm/s的速度向点O运动,设点P在整个运动过程中的时间为t,则t的最小值是2$\sqrt{3}$s. 如图是甲、乙、丙三人玩跷跷板的示意图(支点在中点处),则甲的体重的取值范围在数轴上表示正确的是( )
如图是甲、乙、丙三人玩跷跷板的示意图(支点在中点处),则甲的体重的取值范围在数轴上表示正确的是( )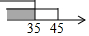


 如图,正方形ABCD中,M为BC上一点,F是AM的中点,EF⊥AM,垂足为F,交AD的延长线于点E,交DC于点N.
如图,正方形ABCD中,M为BC上一点,F是AM的中点,EF⊥AM,垂足为F,交AD的延长线于点E,交DC于点N.