题目内容
9.已知三角形两边的长分别是6和12,则此三角形第三边的长可能是( )| A. | 5 | B. | 6 | C. | 11 | D. | 18 |
分析 已知三角形的两边长分别为6和12,根据在三角形中任意两边之和>第三边,任意两边之差<第三边;即可求第三边长的范围.
解答 解:设第三边长为x,则由三角形三边关系定理得12-6<x<12+6,即6<x<18.
因此,本题的第三边应满足6<x<18,把各项代入不等式符合的即为答案.
只有11符合不等式,
故选C.
点评 此题考查了三角形的三边关系,是求三角形第三边的范围的题,实际上就是根据三角形三边关系定理列出不等式,然后解不等式即可.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
20.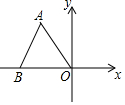 等边△ABO在平面直角坐标系内的位置如图所示,已知△ABO的边长为6,则点A的坐标为( )
等边△ABO在平面直角坐标系内的位置如图所示,已知△ABO的边长为6,则点A的坐标为( )
 等边△ABO在平面直角坐标系内的位置如图所示,已知△ABO的边长为6,则点A的坐标为( )
等边△ABO在平面直角坐标系内的位置如图所示,已知△ABO的边长为6,则点A的坐标为( )| A. | (-3,3) | B. | (3,-3$\sqrt{3}$) | C. | (-3,3$\sqrt{3}$) | D. | (-3,-3$\sqrt{3}$) |
17.下列各组整式中,不是同类项的是( )
| A. | 3x3y与xy3 | B. | -2016与2017 | C. | 4ab2与-3ab2 | D. | 2ab与1020ab |
14.某工厂现在平均每天比原计划多生产10台机器,现在生产700台机器所需时间与原计划生产500台机器所需时间相同,设原计划平均每天生产x台机器,根据题意列方程得( )
| A. | $\frac{700}{x}$=$\frac{500}{x+10}$ | B. | $\frac{700}{x-10}$=$\frac{500}{x}$ | C. | $\frac{700}{x}$=$\frac{500}{x-10}$ | D. | $\frac{700}{x+10}$=$\frac{500}{x}$ |
18.学校举行广播操比赛,八年级三个班的各项得分及三项得分的平均数如下(单位:分).
根据表中信息回答下列问题:
(1)学校将“服装统一”、“队形整齐”、“动作规范”三项按2:3:5的比例计算各班成绩,求八年级三个班的成绩;
(2)由表中三项得分的平均数可知二班排名第一,在(1)的条件下,二班成绩的排名发生了变化,请你说明二班成绩排名发生变化的原因.
| 服装统一 | 进退场有序 | 动作规范 | 动作整齐 | |
| 一班 | 80 | 84 | 88 | 84 |
| 二班 | 97 | 78 | 80 | 85 |
| 三班 | 90 | 78 | 84 | 84 |
(1)学校将“服装统一”、“队形整齐”、“动作规范”三项按2:3:5的比例计算各班成绩,求八年级三个班的成绩;
(2)由表中三项得分的平均数可知二班排名第一,在(1)的条件下,二班成绩的排名发生了变化,请你说明二班成绩排名发生变化的原因.
19.己知一次函数y=kx+b的图象经过第一、二、四象限,则b的值可能是( )
| A. | 2 | B. | 0 | C. | -1 | D. | -2 |
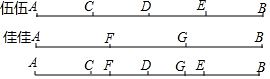 在学习了线段的相关知识后,伍伍与佳佳对一根细绳AB进行了如下研究:伍伍把细绳AB折叠,找到了它的三个四等分点,分别为C、D、E;佳佳再把细绳AB进行折叠,找到了它的两个三等分点,分别为F、G,如图所示,伍伍度量出CF=5厘米,求细绳AB的长度.
在学习了线段的相关知识后,伍伍与佳佳对一根细绳AB进行了如下研究:伍伍把细绳AB折叠,找到了它的三个四等分点,分别为C、D、E;佳佳再把细绳AB进行折叠,找到了它的两个三等分点,分别为F、G,如图所示,伍伍度量出CF=5厘米,求细绳AB的长度.