题目内容
10. 如图,⊙O的半径为4,△ABC是⊙O的内接三角形,连接OB、OC,若∠BAC与∠BOC互补,则弦BC的长为( )
如图,⊙O的半径为4,△ABC是⊙O的内接三角形,连接OB、OC,若∠BAC与∠BOC互补,则弦BC的长为( )| A. | 7$\sqrt{3}$ | B. | 6$\sqrt{3}$ | C. | 5$\sqrt{3}$ | D. | 4$\sqrt{3}$ |
分析 作OH⊥BC于H,首先证明∠BOC=120,在Rt△BOH中,BH=OB•sin60°=4×$\frac{\sqrt{3}}{2}$=2$\sqrt{3}$,即可推出BC=2BH=4$\sqrt{3}$,
解答 解:作OH⊥BC于H.
∵∠BOC=2∠BAC,∠BOC+∠BAC=180°,
∴∠BOC=120°,
∵OH⊥BC,OB=OC,
∴BH=HC,∠BOH=∠HOC=60°,
在Rt△BOH中,BH=OB•sin60°=4×$\frac{\sqrt{3}}{2}$=2$\sqrt{3}$,
∴BC=2BH=4$\sqrt{3}$,
故选D.
点评 本题考查三角形的外接圆与外心、锐角三角函数、垂径定理等知识,解题的关键是学会添加常用辅助线,还在直角三角形解决问题,属于中考常考题型.

练习册系列答案
相关题目
20.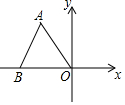 等边△ABO在平面直角坐标系内的位置如图所示,已知△ABO的边长为6,则点A的坐标为( )
等边△ABO在平面直角坐标系内的位置如图所示,已知△ABO的边长为6,则点A的坐标为( )
 等边△ABO在平面直角坐标系内的位置如图所示,已知△ABO的边长为6,则点A的坐标为( )
等边△ABO在平面直角坐标系内的位置如图所示,已知△ABO的边长为6,则点A的坐标为( )| A. | (-3,3) | B. | (3,-3$\sqrt{3}$) | C. | (-3,3$\sqrt{3}$) | D. | (-3,-3$\sqrt{3}$) |
18.学校举行广播操比赛,八年级三个班的各项得分及三项得分的平均数如下(单位:分).
根据表中信息回答下列问题:
(1)学校将“服装统一”、“队形整齐”、“动作规范”三项按2:3:5的比例计算各班成绩,求八年级三个班的成绩;
(2)由表中三项得分的平均数可知二班排名第一,在(1)的条件下,二班成绩的排名发生了变化,请你说明二班成绩排名发生变化的原因.
| 服装统一 | 进退场有序 | 动作规范 | 动作整齐 | |
| 一班 | 80 | 84 | 88 | 84 |
| 二班 | 97 | 78 | 80 | 85 |
| 三班 | 90 | 78 | 84 | 84 |
(1)学校将“服装统一”、“队形整齐”、“动作规范”三项按2:3:5的比例计算各班成绩,求八年级三个班的成绩;
(2)由表中三项得分的平均数可知二班排名第一,在(1)的条件下,二班成绩的排名发生了变化,请你说明二班成绩排名发生变化的原因.
5.若8x2my3与-3xy2n是同类项,则|2m-2n|的值是( )
| A. | 0 | B. | 2 | C. | 7 | D. | -1 |
19.己知一次函数y=kx+b的图象经过第一、二、四象限,则b的值可能是( )
| A. | 2 | B. | 0 | C. | -1 | D. | -2 |
20. 数轴上的A,B,C,D四个点中,离表示-$\sqrt{2}$的点最接近的是( )
数轴上的A,B,C,D四个点中,离表示-$\sqrt{2}$的点最接近的是( )
 数轴上的A,B,C,D四个点中,离表示-$\sqrt{2}$的点最接近的是( )
数轴上的A,B,C,D四个点中,离表示-$\sqrt{2}$的点最接近的是( )| A. | 点A | B. | 点B | C. | 点C | D. | 点D |
 如图,一个表面涂满颜色的正方体,现将每条棱三等分,再把它切开变成若干个小正方体,两面都涂色的有12个.
如图,一个表面涂满颜色的正方体,现将每条棱三等分,再把它切开变成若干个小正方体,两面都涂色的有12个. 如图,在△ABC中,∠ABC=50°,∠ACB=80°,BP平分∠ABC,CP平分∠ACB,求∠BPC的大小.
如图,在△ABC中,∠ABC=50°,∠ACB=80°,BP平分∠ABC,CP平分∠ACB,求∠BPC的大小.