题目内容
15. 如图,正方形ABCD中,M为BC上一点,F是AM的中点,EF⊥AM,垂足为F,交AD的延长线于点E,交DC于点N.
如图,正方形ABCD中,M为BC上一点,F是AM的中点,EF⊥AM,垂足为F,交AD的延长线于点E,交DC于点N.求证:△ABM∽△EFA.
分析 先利用矩形的性质得∠B=90°,AD∥BC,则利用平行线的性质得∠AMB=∠EAF,然后根据有两组角对应相等的两个三角形相似可判定△ABM∽△EFA.
解答 证明:∵四边形ABCD为平行四边形,
∴∠B=90°,AD∥BC,
∴∠AMB=∠EAF,
∵EF⊥AM,
∴∠AFE=90°,
∴∠B=∠AFE,
∴△ABM∽△EFA.
点评 本题考查了相似三角形的判定:有两组角对应相等的两个三角形相似.也考查了矩形的性质.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6. 盘秤是一种常见的称量工具,指针转过的角度与被称物体的重量有一定的关系,如下表所示:
盘秤是一种常见的称量工具,指针转过的角度与被称物体的重量有一定的关系,如下表所示:
(1)请直接写出a、b的值;
(2)指针转过的角度不得超过360°,否则盘秤会受损,称量22千克的物品会对盘秤造成损伤吗?说说你的理由.
(3)某顾客在一家水果店购买水果,用这种盘秤称量两次,第二次的数量是第一次数量的2倍少3千克,且指针第二次转过的角度比第一次大108°,该顾客一共购买了多少千克水果?
 盘秤是一种常见的称量工具,指针转过的角度与被称物体的重量有一定的关系,如下表所示:
盘秤是一种常见的称量工具,指针转过的角度与被称物体的重量有一定的关系,如下表所示:| 重量(单位:千克) | 0 | 1 | 2 | 2.5 | 3 | … | b |
| 指针转过的角度 | 0° | 18° | 36° | a° | 54° | … | 180° |
(2)指针转过的角度不得超过360°,否则盘秤会受损,称量22千克的物品会对盘秤造成损伤吗?说说你的理由.
(3)某顾客在一家水果店购买水果,用这种盘秤称量两次,第二次的数量是第一次数量的2倍少3千克,且指针第二次转过的角度比第一次大108°,该顾客一共购买了多少千克水果?
20.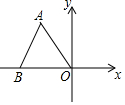 等边△ABO在平面直角坐标系内的位置如图所示,已知△ABO的边长为6,则点A的坐标为( )
等边△ABO在平面直角坐标系内的位置如图所示,已知△ABO的边长为6,则点A的坐标为( )
 等边△ABO在平面直角坐标系内的位置如图所示,已知△ABO的边长为6,则点A的坐标为( )
等边△ABO在平面直角坐标系内的位置如图所示,已知△ABO的边长为6,则点A的坐标为( )| A. | (-3,3) | B. | (3,-3$\sqrt{3}$) | C. | (-3,3$\sqrt{3}$) | D. | (-3,-3$\sqrt{3}$) |
5.若8x2my3与-3xy2n是同类项,则|2m-2n|的值是( )
| A. | 0 | B. | 2 | C. | 7 | D. | -1 |
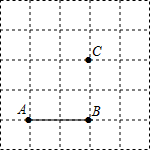 如图,己知线段AB及点C,在方格纸上画图并回答问题.
如图,己知线段AB及点C,在方格纸上画图并回答问题.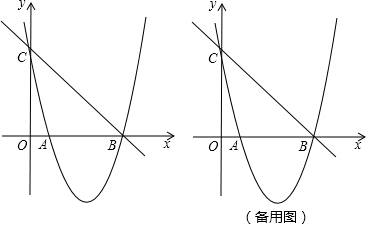
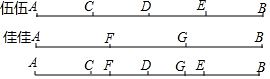 在学习了线段的相关知识后,伍伍与佳佳对一根细绳AB进行了如下研究:伍伍把细绳AB折叠,找到了它的三个四等分点,分别为C、D、E;佳佳再把细绳AB进行折叠,找到了它的两个三等分点,分别为F、G,如图所示,伍伍度量出CF=5厘米,求细绳AB的长度.
在学习了线段的相关知识后,伍伍与佳佳对一根细绳AB进行了如下研究:伍伍把细绳AB折叠,找到了它的三个四等分点,分别为C、D、E;佳佳再把细绳AB进行折叠,找到了它的两个三等分点,分别为F、G,如图所示,伍伍度量出CF=5厘米,求细绳AB的长度.