题目内容
15.抛物线y=x2-2x+1,则图象与x轴交点为( )| A. | 二个交点 | B. | 一个交点 | C. | 无交点 | D. | 不能确定 |
分析 直接利用b2-4ac的符号进而得出抛物线与x轴交点个数即可.
解答 解:∵b2-4ac=(-2)2-4×1×1=0,
∴抛物线y=-x2+2kx+2与x轴交点的个数为:1.
故选B.
点评 此题主要考查了抛物线与x轴交点,得出b2-4ac的符号是解题关键.

练习册系列答案
相关题目
6.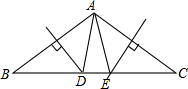 如图,△ABC中,AB、AC的垂直平分线分别交BC于D、E,且∠DAE=20°,则∠BAC=( )
如图,△ABC中,AB、AC的垂直平分线分别交BC于D、E,且∠DAE=20°,则∠BAC=( )
 如图,△ABC中,AB、AC的垂直平分线分别交BC于D、E,且∠DAE=20°,则∠BAC=( )
如图,△ABC中,AB、AC的垂直平分线分别交BC于D、E,且∠DAE=20°,则∠BAC=( )| A. | 100° | B. | 120° | C. | 150° | D. | 160° |
10.若△ABC的三边a,b,c满足a2+b2-8a-10b+29+|c-3|=0,则( )
| A. | △ABC是直角三角形且∠C=90° | B. | △ABC是锐角三角形 | ||
| C. | △ABC是直角三角形且∠B=90° | D. | △ABC是直角三角形且∠A=90° |
7.下列方程是关于x的一元二次方程的是( )
| A. | ax2+bx+c=0 | B. | $\frac{1}{{x}^{2}}+\frac{1}{x}$=2 | C. | x2+2x=x2-1 | D. | 3(x+1)2=2(x+1) |
4.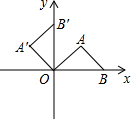 将等腰直角三角形AOB按如图所示放置,然后绕点O逆时针旋转90°至△A′OB′的位置,点B的横坐标为2,则点A′的坐标为( )
将等腰直角三角形AOB按如图所示放置,然后绕点O逆时针旋转90°至△A′OB′的位置,点B的横坐标为2,则点A′的坐标为( )
 将等腰直角三角形AOB按如图所示放置,然后绕点O逆时针旋转90°至△A′OB′的位置,点B的横坐标为2,则点A′的坐标为( )
将等腰直角三角形AOB按如图所示放置,然后绕点O逆时针旋转90°至△A′OB′的位置,点B的横坐标为2,则点A′的坐标为( )| A. | (1,1) | B. | (-1,1) | C. | (1,-1) | D. | $(-\sqrt{2},\sqrt{2})$ |
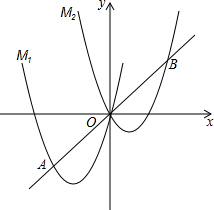 如图,将抛物线M1:y1=ax2+4x向右平移3个单位,再向上平移3个单位,得到抛物线y2,记为M2,直线y=x与M1
如图,将抛物线M1:y1=ax2+4x向右平移3个单位,再向上平移3个单位,得到抛物线y2,记为M2,直线y=x与M1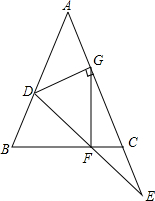 如图,在△ABC中,AB=AC,D是AB上一点,点E在AC的延长线上,且BD=CE,连结DE交BC于F,过点D作DG⊥AE,垂足为G,连结FG.若FG=$\sqrt{2}$,∠E=30°,则GE=$\sqrt{6}$.
如图,在△ABC中,AB=AC,D是AB上一点,点E在AC的延长线上,且BD=CE,连结DE交BC于F,过点D作DG⊥AE,垂足为G,连结FG.若FG=$\sqrt{2}$,∠E=30°,则GE=$\sqrt{6}$.