题目内容
3.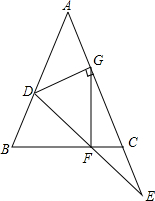 如图,在△ABC中,AB=AC,D是AB上一点,点E在AC的延长线上,且BD=CE,连结DE交BC于F,过点D作DG⊥AE,垂足为G,连结FG.若FG=$\sqrt{2}$,∠E=30°,则GE=$\sqrt{6}$.
如图,在△ABC中,AB=AC,D是AB上一点,点E在AC的延长线上,且BD=CE,连结DE交BC于F,过点D作DG⊥AE,垂足为G,连结FG.若FG=$\sqrt{2}$,∠E=30°,则GE=$\sqrt{6}$.
分析 作DH∥AC交BC于H,如图,利用等腰三角形的性质得∠B=∠ACB,再根据平行线的性质得∠BHD=∠ACB,则∠B=∠BHD,所以DB=DH,加上DB=CE,所以DH=CE,于是可根据“AAS”可证明△DHF≌△ECF,得到DF=EF,则GF为斜边DE上的中线,所以DE=2GF=2$\sqrt{2}$,然后根据含30度的直角三角形三边的关系可求出GE.
解答  解:作DH∥AC交BC于H,如图,
解:作DH∥AC交BC于H,如图,
∵AB=AC,
∴∠B=∠ACB,
∵DH∥AC,
∴∠BHD=∠ACB,∠E=∠EDH,
∴∠B=∠BHD,
∴DB=DH,
而DB=CE,
∴DH=CE,
在△DHF和△ECF中,
$\left\{\begin{array}{l}{∠DFH=∠EFC}\\{∠FDH=∠E}\\{DH=EC}\end{array}\right.$,
∴△DHF≌△ECF,
∴DF=EF,
∵DG⊥AC,
∴∠DGE=90°,
∵GF为斜边DE上的中线,
∴DE=2GF=2$\sqrt{2}$,
而∠E=30°,
∴DG=$\frac{1}{2}$DE=$\sqrt{2}$,
∴GE=$\sqrt{3}$DG=$\sqrt{6}$.
故答案为$\sqrt{6}$.
点评 本题考查了全等三角形的判定与性质:全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.在判定三角形全等时,关键是选择恰当的判定条件.在应用全等三角形的判定时,要注意三角形间的公共边和公共角,必要时添加适当辅助线构造三角形.也考查了含30度的直角三角形三边的关系.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
11.小王每个周一到周五的早上都会乘坐石家庄的110路公交车从柏林庄站到棉六站,小王统计了他40次乘坐的110路公交车在此路段上行驶的时间,并把数据分组整理,结果如下表,利用组中值,可得小王40次乘坐110路公交车所用的平均时间为4min.
| 时间t/min | 12≤t<16 | 16≤t<20 | 20≤t<24 | 24≤t<28 | 合计 |
| 次数 | 6 | 12 | 14 | 8 | 40 |
15.抛物线y=x2-2x+1,则图象与x轴交点为( )
| A. | 二个交点 | B. | 一个交点 | C. | 无交点 | D. | 不能确定 |