如果多项式x2-5x+m分解因式的结果为.那么m.n的值分别为( )A．m=-2.n=6B．m=2.n=-6C．m=6.n=-2D．m=-6.n=-2 题目和参考答案——青夏教育精英家教网—

题目内容

4．如果多项式x²-5x+m分解因式的结果为（x-3）（x+n），那么m，n的值分别为（　　）

A．

m=-2，n=6

B．

m=2，n=-6

C．

m=6，n=-2

D．

m=-6，n=-2

分析根据因式分解是把一个多项式转化成几个整式乘积的形式，可得m、n的值．

解答解：∵多项式x²-5x+m分解因式的结果为（x-3）（x+n），
∴-3+n=-5，-3n=m
解得m=6，n=-2，
故选：C．

点评本题考查了十字相乘法分解因式，运用十字相乘法分解因式时，要注意观察，尝试，并体会它实质是二项式乘法的逆过程．

练习册系列答案

	A．	a的系数为0		B．	ab²c的次数是2
	C．	$\frac{1}{2}$πxy³的系数为$\frac{1}{2}$π		D．	-5是一次单项式

12．计算：-2a（a²-1）的结果是-2a³+2a．

19．如果二次三项式x²-6mx+9是一个完全平方式，那么m的值为±1．

2．

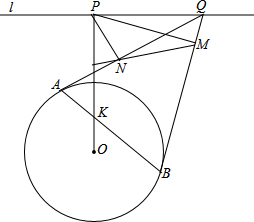如图，圆O（圆心为O）与直线l相离，作OP⊥l，P为垂足．设点Q是l上任意一点（不与点P重合），过点Q作圆O的两条切线QA和QB，A和B为切点，AB与OP相交于点K．过点P作PM⊥QB，PN⊥QA，M和N为垂足．求证：直线MN平分线段KP．

9．如图所示，A，B是坐标轴正半轴上的两点，过点B作PB⊥y轴交双曲线y=$\frac{6}{x}$（x＞0）于P点，A，B两点的坐标分别为（1，0），（0，3），x轴上的动点M在点A的右侧，动点N在射线BP上，过点A作AB的垂线，交射线BP于D点，交直线MN于Q点，连结BQ，取BQ的中点C，若以A，C，N，Q为顶点的四边形是平行四边形，则Q点的坐标为（4，1）或（28，9）．

6．（1）x²-4x-6=0
（2）3x（x+2）-5（x+2）=0．

7．y=-（x+1）²+k上有A（-$\sqrt{2}$，y₁），B（$\sqrt{2}$，y₂）两点，则y₁，y₂的大小关系为（　　）

y₁＞y₂

y₁＜y₂

y₁≥y₂

y₁≤y₂

试题分类