题目内容
1.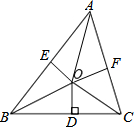 如图,已知△ABC的周长是21,OB、OC分别平分∠ABC和∠ACB,OD⊥BC于D,OE⊥AB,OF⊥AC,且OD=3.
如图,已知△ABC的周长是21,OB、OC分别平分∠ABC和∠ACB,OD⊥BC于D,OE⊥AB,OF⊥AC,且OD=3.(1)试判断线段OD、OE、OF的大小关系.
(2)求△ABC的面积.
分析 (1)根据角平分线的性质解答;
(2)根据三角形的面积公式计算即可.
解答 解:(1)OD=OE=OF.
∵OB、OC分别平分∠ABC和∠ACB,OD⊥BC于D,OE⊥AB,OF⊥AC,
∴OE=OD=3,OF=OD=3,
∴OD=OE=OF;
(2)△ABC的面积=$\frac{1}{2}$×(AB+AC+BC)×OD=$\frac{1}{2}$×21×2=21.
点评 本题考查的是角平分线的性质,掌握角的平分线上的点到角的两边的距离相等是解题的关键.

练习册系列答案
相关题目
12.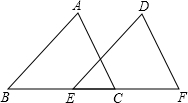 如图,在△ABC和△DEF中,∠B=∠DEF,AB=DE,添加下列一个条件后,仍然不能证明△ABC≌△DEF,这个条件是( )
如图,在△ABC和△DEF中,∠B=∠DEF,AB=DE,添加下列一个条件后,仍然不能证明△ABC≌△DEF,这个条件是( )
 如图,在△ABC和△DEF中,∠B=∠DEF,AB=DE,添加下列一个条件后,仍然不能证明△ABC≌△DEF,这个条件是( )
如图,在△ABC和△DEF中,∠B=∠DEF,AB=DE,添加下列一个条件后,仍然不能证明△ABC≌△DEF,这个条件是( )| A. | ∠A=∠D | B. | BE=FC | C. | ∠ACB=∠F | D. | AC=DF |
6.下列汽车标志中,是轴对称图形的个数有( )个.


| A. | 4个 | B. | 5个 | C. | 6个 | D. | 7个 |
10.下列函数中,反比例函数是( )
| A. | $y=\frac{x}{3}$ | B. | y=$\frac{1}{x+1}$ | C. | y=$\frac{1}{2}$x | D. | y=$\frac{1}{3x}$ |
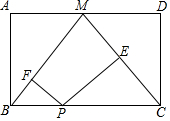 如图,M是矩形ABCD的边AD的中点,P为BC上一点,PE⊥MC,PF⊥MB,垂足分别为E,F,当AB,BC满足什么条件时,四边形PEMF为矩形?试加以证明.
如图,M是矩形ABCD的边AD的中点,P为BC上一点,PE⊥MC,PF⊥MB,垂足分别为E,F,当AB,BC满足什么条件时,四边形PEMF为矩形?试加以证明.