题目内容
14.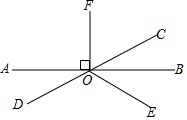 如图,已知AB、CD相交于点O,OB平分∠COE,OF⊥AB于O,
如图,已知AB、CD相交于点O,OB平分∠COE,OF⊥AB于O,(1)若∠EOF=120°,求∠AOD的度数;
(2)若∠BOE=$\frac{1}{4}$∠EOF,求∠DOE的度数.
分析 (1)直接利用垂直的定义结合角平分线的定义得出∠AOD的度数;
(2)直接利用垂直的定义结合角平分线的定义得出∠COE=2∠BOE,进而得出∠DOE的度数.
解答 解:(1)∵OF⊥AB ∴∠BOF=90°
∴∠BOF=90°
又∵∠EOF=120°
∴∠BOE=∠EOF-∠BOF=30°
∵OB平分∠COE
∴∠BOC=∠BOE=30°
∵∠AOD=∠BOC
∴∠BOC=30°;
(2)∵∠BOE=$\frac{1}{4}$∠EOF
∴∠EOF=4∠BOE
∵∠BOF=∠EOF-∠BOE
∴∠BOF=4∠BOE-∠BOE=3∠BOE
∵∠BOF=90°
∴3∠BOE=90°
∴∠BOE=30°
∵OB平分∠COE
∴∠COE=2∠BOE=60°
∴∠DOE=180°-∠COE=120°.
点评 此题主要考查了垂线以及角平分线的定义等知识,正确应用角平分线的定义是解题关键.

练习册系列答案
相关题目
4.下列计算正确的是( )
| A. | $\sqrt{3}+\sqrt{2}=\sqrt{5}$ | B. | $\sqrt{2}×\sqrt{5}=\sqrt{10}$ | C. | $\sqrt{8}-\sqrt{2}=\sqrt{6}$ | D. | $\sqrt{8}÷\sqrt{2}=4$ |
2.用“描点法”画二次函数y=ax2+bx+c(a≠0)的图象时,列出了表格:那么该二次函数有最小(填“大”或“小”)值-1.
| x | … | 1 | 2 | 3 | 4 | … |
| y=ax2+bx+c | … | 0 | -1 | 0 | 3 | … |
4.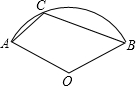 如图,扇形OAB的圆心角为120°,C是弧AB上一点,则∠ACB的度数为( )
如图,扇形OAB的圆心角为120°,C是弧AB上一点,则∠ACB的度数为( )
 如图,扇形OAB的圆心角为120°,C是弧AB上一点,则∠ACB的度数为( )
如图,扇形OAB的圆心角为120°,C是弧AB上一点,则∠ACB的度数为( )| A. | 240° | B. | 120° | C. | 90° | D. | 75° |
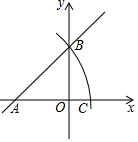 如图,在平面直角坐标系中,直线y=x+b交x轴于点A,交y轴于点B,以点A为圆心,线段AB长为半径作圆弧,交x轴正半轴于点C,若AC=$\sqrt{2}$,则b的值为1.
如图,在平面直角坐标系中,直线y=x+b交x轴于点A,交y轴于点B,以点A为圆心,线段AB长为半径作圆弧,交x轴正半轴于点C,若AC=$\sqrt{2}$,则b的值为1. 如图,矩形ABCD中,AB=8cm,BC=6cm,动点P从点A出发,以每秒3cm的速度沿线段AB向点B运动,连接DP,把∠A沿DP折叠,使点A落在点A′处.求出当△BPA′为直角三角形时,AP=3或6cm.
如图,矩形ABCD中,AB=8cm,BC=6cm,动点P从点A出发,以每秒3cm的速度沿线段AB向点B运动,连接DP,把∠A沿DP折叠,使点A落在点A′处.求出当△BPA′为直角三角形时,AP=3或6cm.