题目内容
3. 如图,矩形ABCD中,AB=8cm,BC=6cm,动点P从点A出发,以每秒3cm的速度沿线段AB向点B运动,连接DP,把∠A沿DP折叠,使点A落在点A′处.求出当△BPA′为直角三角形时,AP=3或6cm.
如图,矩形ABCD中,AB=8cm,BC=6cm,动点P从点A出发,以每秒3cm的速度沿线段AB向点B运动,连接DP,把∠A沿DP折叠,使点A落在点A′处.求出当△BPA′为直角三角形时,AP=3或6cm.
分析 分三种情况进行讨论,当A′、P、B分别为直角顶点时,求出AP的长即可.
解答 解:(1)当∠B A′P=90°时,由折叠得,∠PA′D=∠A=90° ,
,
∴∠BA′D=∠B A′P+∠P A′D=180°,
∴点B、A′、D在一直线上,
设AP=x cm,
∴A′P=x,BP=8-x,A′B=10-6=4,
在Rt△A′PB中,
x2+42=(8-x)2,
解之得:x=3,
即AP=3cm;
(2)当∠A′P B=90°时,
∴∠A′P A=90°,
又∵∠DA′P=∠A=90°,
∴四边形APA′D是矩形,
根据折叠的性质,A′P=AP,
∴四边形APA′D是正方形,
∴AP=AD=6cm;
(3)当∠A′B P=90°时,不存在.
综上所述,当△BPA′为直角三角形时,AP=3或6cm.
故答案为3或6.
点评 本题考查了折叠问题:折叠前后两图形全等,即对应线段相等;对应角相等.也考查了矩形的性质以及勾股定理.注意本题需要分类讨论,避免漏解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
8. 如图,AB∥PD,∠PAB=65°,∠PBA=78°,则∠APB的大小为( )
如图,AB∥PD,∠PAB=65°,∠PBA=78°,则∠APB的大小为( )
 如图,AB∥PD,∠PAB=65°,∠PBA=78°,则∠APB的大小为( )
如图,AB∥PD,∠PAB=65°,∠PBA=78°,则∠APB的大小为( )| A. | 71.5° | B. | 39° | C. | 37° | D. | 32.5° |
13. 如图,如果CD是Rt△ABC的中线,∠ACB=90°,∠A=50°,那么∠CDB等于( )
如图,如果CD是Rt△ABC的中线,∠ACB=90°,∠A=50°,那么∠CDB等于( )
 如图,如果CD是Rt△ABC的中线,∠ACB=90°,∠A=50°,那么∠CDB等于( )
如图,如果CD是Rt△ABC的中线,∠ACB=90°,∠A=50°,那么∠CDB等于( )| A. | 100° | B. | 110° | C. | 120° | D. | 130° |
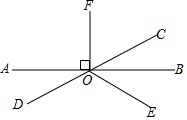 如图,已知AB、CD相交于点O,OB平分∠COE,OF⊥AB于O,
如图,已知AB、CD相交于点O,OB平分∠COE,OF⊥AB于O, 如图,在矩形ABCD中,E在AD上,F在AB上,且EF⊥EC,EF=EC,DE=2,矩形ABCD的周长为16,则AE的长是3.
如图,在矩形ABCD中,E在AD上,F在AB上,且EF⊥EC,EF=EC,DE=2,矩形ABCD的周长为16,则AE的长是3.