题目内容
19．已知关于x，y的方程组$\left\{\begin{array}{l}{3x-5y=2a}\\{x-2y=a-5}\end{array}\right.$，①当a=5时，方程组的解是$\left\{\begin{array}{l}{x=10}\\{y=20}\end{array}\right.$；②当x，y的值互为相反数时，a=20；③不存在一个实数a使得x=y；④若25a-y=2-3，则a=2．其中正确的是②③④（填序号）分析 根据题目各个结论的条件代入原方程组中，可以计算出相应的结论，从而可以解答本题．
解答 解：当a=5时，$\left\{\begin{array}{l}{3x-5y=10}\\{x-2y=0}\end{array}\right.$，解得，$\left\{\begin{array}{l}{x=20}\\{y=10}\end{array}\right.$，故①错误，
当x与y互为相反数时，则x=-y，
∴$\left\{\begin{array}{l}{3x+5x=2a}\\{x+2x=a-5}\end{array}\right.$，得$\left\{\begin{array}{l}{x=5}\\{a=20}\end{array}\right.$，故②正确，
当x=y时，则$\left\{\begin{array}{l}{3x-5x=2a}\\{x-2x=a-5}\end{array}\right.$无解，故③正确，
当25a-y=2-3时，
则$\left\{\begin{array}{l}{3x-5y=2a}\\{x-2y=a-5}\\{5a-y=-3}\end{array}\right.$，得a=2，故④正确，
故答案为：②③④．
点评 本题考查二元一次方程组的解、负整数指数幂，解答本题的关键是明确题意，找出所求问题需要的条件，判断题目中的结论是否成立．
练习册系列答案
相关题目
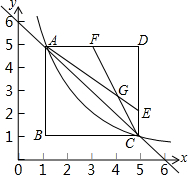如图，若直线y=-x+6与反比例函数y=$\frac{k}{x}$（x＞0）的图象交于A（1，m）与C（n，1）两点，以线段AC为斜边，在AC的两侧作等腰直角三角形ABC和ADC，其中∠B=∠D=90°，F为AD的中点，点E在边CD上，且DE=3EC，AE与CF相交于点G．
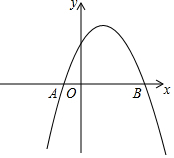如图，已知抛物线y=-x2+bx+c经过A（-1，0），B（3，0）两点．
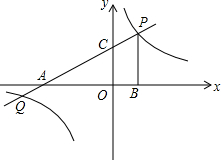如图，直线y=$\frac{1}{2}$x+b，分别交x轴，y轴于点A、C，点P是直线AC与双曲线y=$\frac{k}{x}$在第一象限内的交点，过点P作PB⊥x轴于点B，若OB=2，PB=3