题目内容
10.有6张看上去无差别的卡片,上面分别写着1,2,3,4,5,6,随机抽取1张后,放回并混在一起,再随机抽取1张,则两次取出的数字都是奇数的概率为$\frac{1}{4}$.分析 画树状图展示所有36种等可能的结果数,再找出两次抽取的数字都是奇数的结果数,然后根据概率公式求解.
解答 解:画树状图为:
共有36种等可能的结果数,其中两次抽取的数字都是奇数的结果数为9,
所以随机抽取一张,两次抽取的数字都是奇数的概率=$\frac{9}{36}$=$\frac{1}{4}$.
故答案为:$\frac{1}{4}$.
点评 本题考查了列表法与树状图法:通过列表法或树状图法展示所有等可能的结果求出n,再从中选出符合事件A或B的结果数目m,然后根据概率公式求出事件A或B的概率.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.若实数a满足等式|1-a|=1+|a|,则$\sqrt{(a-1)^{2}}$=( )
| A. | 1 | B. | -a-1 | C. | a-1 | D. | 1-a |
18. 如图,在△ABC中,∠C=90°,分别以点A、B为圆心,大于$\frac{1}{2}$AB长为半径作弧,两弧分别交于M、N两点,过M、N两点的直线交AC于点E,若AC=6,BC=3,则CE的长为( )
如图,在△ABC中,∠C=90°,分别以点A、B为圆心,大于$\frac{1}{2}$AB长为半径作弧,两弧分别交于M、N两点,过M、N两点的直线交AC于点E,若AC=6,BC=3,则CE的长为( )
 如图,在△ABC中,∠C=90°,分别以点A、B为圆心,大于$\frac{1}{2}$AB长为半径作弧,两弧分别交于M、N两点,过M、N两点的直线交AC于点E,若AC=6,BC=3,则CE的长为( )
如图,在△ABC中,∠C=90°,分别以点A、B为圆心,大于$\frac{1}{2}$AB长为半径作弧,两弧分别交于M、N两点,过M、N两点的直线交AC于点E,若AC=6,BC=3,则CE的长为( )| A. | $\frac{9}{4}$ | B. | $\frac{11}{2}$ | C. | $\sqrt{3}$ | D. | $\frac{3}{2}$ |
15.下列四组线段中,能组成直角三角形的是( )
| A. | a=2,b=2,c=3 | B. | a=2,b=3,c=4 | C. | a=4,b=5,c=6 | D. | a=5,b=12,c=13 |
19.下列运算正确的是( )
| A. | a6÷a3=a2 | B. | (-2a)3=-8a3 | C. | a6•a4=a24 | D. | (a3)3=a6 |
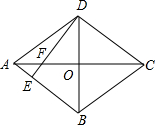 如图,菱形ABCD中,AC=8,BD=6,DE⊥AB,交AC于点F,则EF=$\frac{21}{20}$.
如图,菱形ABCD中,AC=8,BD=6,DE⊥AB,交AC于点F,则EF=$\frac{21}{20}$.