题目内容
5.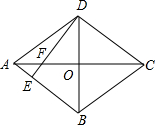 如图,菱形ABCD中,AC=8,BD=6,DE⊥AB,交AC于点F,则EF=$\frac{21}{20}$.
如图,菱形ABCD中,AC=8,BD=6,DE⊥AB,交AC于点F,则EF=$\frac{21}{20}$.
分析 根据“菱形的面积等于对角线乘积的一半”可以求得该菱形的面积.菱形的面积还等于底乘以高,求出可得DE的长度,再由勾股定理求出AE,证明△AEF∽△AOB,得出对应边成比例,即可求出EF的长.
解答 解:∵四边形ABCD是菱形,AC=8,BD=6,AB=AD,
∴AC⊥OD,AO=$\frac{1}{2}$AC=4,BO=$\frac{1}{2}$BD=3,
∴由勾股定理得到:AD=AB=$\sqrt{A{O}^{2}+B{O}^{2}}$=5,
又∵DE⊥AB,
∴$\frac{1}{2}$AC•BD=AB•DE.
∴DE=$\frac{AC•BD}{2AB}$=$\frac{8×6}{2×5}$=$\frac{24}{5}$.
∴AE=$\sqrt{A{D}^{2}-D{E}^{2}}$=$\frac{7}{5}$,
∵∠AOB=∠AEF=90°,∠EAF=∠OAB,
∴△AEF∽△AOB,
∴$\frac{EF}{BO}=\frac{AE}{AO}$,
即$\frac{EF}{3}=\frac{\frac{7}{5}}{4}$,
解得:EF=$\frac{21}{20}$;
故答案为:$\frac{21}{20}$.
点评 本题考查了菱形的性质、勾股定理、相似三角形的判定与性质、菱形面积的计算;熟练掌握菱形的性质,证明三角形相似是解决问题的关键.

练习册系列答案
相关题目
14.下列四个式子中,属于代数式的是( )
| A. | x+y=y+x | B. | -a | C. | S=$\frac{1}{2}ah$ | D. | 3x-1>0 |
17.10名射击运动员第一轮比赛的成绩如表所示:
则他们本轮比赛的平均成绩是8.4(环)
| 环数 | 7 | 8 | 9 | 10 |
| 人数 | 3 | 2 | 3 | 2 |
14.已知,函数y=3x的图象经过点A(1,y1),点B(-2,y2),则( )
| A. | y1>y2 | B. | y1<y2 | ||
| C. | y1=y2 | D. | y1、y2无法比较大小 |
15.对多项式a2-1因式分解,正确的是( )
| A. | a2-1=(a+1)2 | B. | a2-1=(a-1)2 | C. | a2-1=(a-1)(a+1) | D. | a2-1=(1-a)(1+a) |