Question

14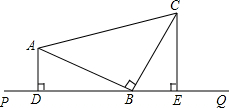．如图，△ABC中，AB=BC，∠ABC=90°，经过B点有一条直线PQ，分别过A、C作AD⊥PQ于D，CE⊥PQ于E．
（1）线段DE、AD、CE满足怎样的数量关系？试证明之；
（2）若直线PQ与线段AC相交，其他条件不变，（1）中关系是否仍然成立？若不成立，写出相应的结论，并证明．

Answer 1

分析 （1）根据已知条件及互余关系可证△ABD≌△BCE，则BD=CE，AD=BE，由DE=BD+BE，得出线段DE=AD+CE．
（2）不成立，如果PQ和AC相交，则DE等于AD和CE的差的绝对值，和（1）相同，证明△ABD全等于△BCE（直角三角形有一边相等，有一对角互余），得到AD=BE，CE=BD，假设AD＞CE，两等式相减即可．

解答 解：（1）∵∠ABD+∠BAD=90°，∠ABD+∠CBE=90°，
∴∠BAD=∠CBE，
又∵AB=AC，∠BDA=∠BEC=90°，
在△ABD和△BCE中，
$\left\{\begin{array}{l}{∠BAD=∠CBE}\\{∠BDA=∠BEC}\\{AB=BC}\end{array}\right.$，
∴△ABD≌△BCE（AAS），
∴BD=CE，AD=BE，
∴DE=BE+BD=AD+CE．
（2）不成立，如果PQ和AC相交，则DE等于AD和CE的差的绝对值，如图，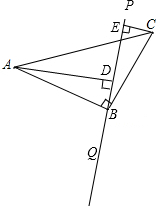

∵∠ABD+∠BAD=90°，∠ABD+∠CBE=90°，
∴∠BAD=∠CBE，
又∵AB=AC，∠BDA=∠BEC=90°，
在△ABD和△BCE中，
$\left\{\begin{array}{l}{∠BAD=∠CBE}\\{∠BDA=∠BEC}\\{AB=BC}\end{array}\right.$，
∴△ABD≌△BCE（AAS），
∴BD=CE，AD=BE，
假设AD＞CE，两等式相减可得：DE=|AD-CE|．

点评 本题考查了全等三角形的判定与性质．解答该题时，围绕结论寻找全等三角形，运用全等三角形的性质判定对应线段相等．