题目内容

6．一列数按某种规律排列为：2，5，10，17，26，…，则第10个数应是101；第n个数应是n2+1．

分析 由2=12+1，5=22+1，10=32+1，17=42+1，26=52+1，…，得出第n个数应是n2+1，由此代入求得答案．

解答 解：∵2=12+1，
5=22+1，
10=32+1，
17=42+1，
26=52+1，
…，
∴第10个数应是102+1=101；第n个数应是n2+1．
故答案为：101，n2+1．

点评 此题考查数字的变化规律，找出数字之间的联系，得出运算规律，利用运算规律解决问题．

练习册系列答案
相关题目
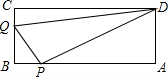16．如图．A、B、C、D为矩形的4个顶点：AB=16cm，BC=6cm，动点P、Q分别从点A、C同时出发，点P以3cm/s的速度向点B移动，一直到达点B为止：点Q以2cm/s的速度向点B移动，经过多长时间P、Q两点之间的距离是10cm？
17．已知2是关于x的方程：x2-x+a=0的一个解，则2a-1的值是（　　）
A．5B．-5C．3D．-3
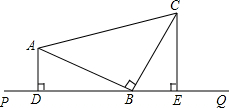14．如图，△ABC中，AB=BC，∠ABC=90°，经过B点有一条直线PQ，分别过A、C作AD⊥PQ于D，CE⊥PQ于E．
（1）线段DE、AD、CE满足怎样的数量关系？试证明之；
（2）若直线PQ与线段AC相交，其他条件不变，（1）中关系是否仍然成立？若不成立，写出相应的结论，并证明．
1．下列计算正确的是（　　）
A．3x3+x3=4x6B．2ab-ab=1
C．xy2-0.2y2x=$\frac{4}{5}$xy2D．4a2+3b2+2ab-4a2-3b2=ab
11．结合你身边的生活实例，自编一道可以通过解方程（组）5x+4（5-2x）=18或$\left\{\begin{array}{l}{5x+4y=18}\\{2x+y=5}\end{array}\right.$的应用题，并写出详细的解答过程．
18．已知，A（4，-1），B（2，-4），在x轴上找一点C，y轴上找一点D，使|AC+CD+BD|最小，求这个最小值．
15．在有些情况下，不需要计算出结果也能把绝对值符号去掉．例如：
|6+7|=6+7；|6-7|=7-6；|7-6|=7-6；|-6-7|=6+7；
根据上面的规律，把下列各式写成去掉绝对值符号的形式：
（1）|7-21|=21-7；
（2）|$-\frac{1}{2}+0.8$|=0.8-$\frac{1}{2}$；
（3）|$\frac{7}{17}-\frac{7}{18}$|=$\frac{7}{17}-\frac{7}{18}$；
（4）|$3.2-2.8-\frac{2}{3}$|=2.8+$\frac{2}{3}$-3.2；
（5）用合理的方法计算：|$\frac{1}{5}-\frac{150}{557}$|+|$\frac{150}{557}-\frac{1}{2}$|-|$\frac{1}{5}$$-\frac{1}{2}$|．
16．下列二次根式中，哪些是最简二次根式？把不是最简二次根式的化成最简二次根式．
（1）$\sqrt{0.2}$；
（2）$\sqrt{\frac{2}{3}ab}$；
（3）$\sqrt{{x}^{2}+1}$；
（4）$\sqrt{32m}$；
（5）$\sqrt{{a}^{3}+6{a}^{2}+9a}$（a＞0）．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网