题目内容
19.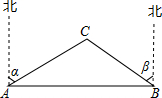 如图,已知A、B两市相距150千米,分别从A、B处测得某风景区中心C处的方向角如图所示,风景区区域是以C为圆心,52千米为半径的圆,tanα≈1.63,tanβ≈1.37.有关部门要设计修建连接AB两市的高速公路,问连接AB的高速公路是否穿过风景区,请说明理由.
如图,已知A、B两市相距150千米,分别从A、B处测得某风景区中心C处的方向角如图所示,风景区区域是以C为圆心,52千米为半径的圆,tanα≈1.63,tanβ≈1.37.有关部门要设计修建连接AB两市的高速公路,问连接AB的高速公路是否穿过风景区,请说明理由.
分析 首先过C作CD⊥AB与D,由题意得∠ACD=α,∠BCD=β,在Rt△ACD中,AD=CD•tanα,在Rt△BCD中,BD=CD•tanβ,继而可得CD•tanα+CD•tanβ=AB,则可求得CD的长,再进行比较,即可得出高速公路是否穿过风景区.
解答 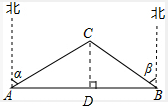 解:AB穿过风景区,理由如下:
解:AB穿过风景区,理由如下:
如图,过C作CD⊥AB于D,
由题意得:∠ACD=α,∠BCD=β,
则AD=CD•tanα,BD=CD•tanβ,
∵AD+BD=AB,
∴CD•tanα+CD•tanβ=AB,
∴CD=$\frac{AB}{tanα+tanβ}$=$\frac{150}{1.63+1.37}$=50(千米),
∵CD=50<52,
∴高速公路AB穿过风景区.
点评 此题考查了方向角问题,能借助于方向角构造直角三角形,并利用解直角三角形的知识求解是解此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8.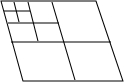 如图,将一个菱形的纸片剪成4个完全相同的小菱形,共得到4个菱形,再将其中1个小菱形剪成4个完全相同的更小的菱形,共得到7个菱形,…,按照此规律,依次操作减剪下去,则第n次剪,会得到菱形的个数为( )
如图,将一个菱形的纸片剪成4个完全相同的小菱形,共得到4个菱形,再将其中1个小菱形剪成4个完全相同的更小的菱形,共得到7个菱形,…,按照此规律,依次操作减剪下去,则第n次剪,会得到菱形的个数为( )
 如图,将一个菱形的纸片剪成4个完全相同的小菱形,共得到4个菱形,再将其中1个小菱形剪成4个完全相同的更小的菱形,共得到7个菱形,…,按照此规律,依次操作减剪下去,则第n次剪,会得到菱形的个数为( )
如图,将一个菱形的纸片剪成4个完全相同的小菱形,共得到4个菱形,再将其中1个小菱形剪成4个完全相同的更小的菱形,共得到7个菱形,…,按照此规律,依次操作减剪下去,则第n次剪,会得到菱形的个数为( )| A. | 2n个 | B. | (2n+1)个 | C. | 3n个 | D. | (3n+1)个 |
 如图,以?ABCD的顶点O为原点,边OC所在直线为x轴,建立平面直角坐标系,顶点A、C的坐标分别是(2,4)、(3,0),过点A的反比例函数y=$\frac{k}{x}$的图象交BC于D,连接AD.
如图,以?ABCD的顶点O为原点,边OC所在直线为x轴,建立平面直角坐标系,顶点A、C的坐标分别是(2,4)、(3,0),过点A的反比例函数y=$\frac{k}{x}$的图象交BC于D,连接AD.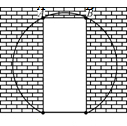 温州外国语学校在进行校园二次美化工程,一面墙上有一个矩形的门洞,如图,已知矩形的高为2米,宽为0.8米,现要将它改为一个圆弧形的门洞,圆弧所在的圆外接于矩形,圆弧所在的圆的半径长为$\frac{2\sqrt{29}}{5}$米.
温州外国语学校在进行校园二次美化工程,一面墙上有一个矩形的门洞,如图,已知矩形的高为2米,宽为0.8米,现要将它改为一个圆弧形的门洞,圆弧所在的圆外接于矩形,圆弧所在的圆的半径长为$\frac{2\sqrt{29}}{5}$米.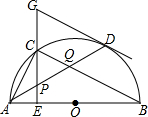 如图,AB是半圆O的直径,D是$\widehat{AB}$上一点,C是$\widehat{AD}$的中点,过点C作AB的垂线,交AB于E,与过点D的切线交于点G,连接AD,分别交CE、CB于点P、Q,连接AC,关于下列结论:
如图,AB是半圆O的直径,D是$\widehat{AB}$上一点,C是$\widehat{AD}$的中点,过点C作AB的垂线,交AB于E,与过点D的切线交于点G,连接AD,分别交CE、CB于点P、Q,连接AC,关于下列结论: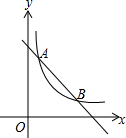 如图,一次函数y=kx+b与反比例函数y=$\frac{m}{x}$(m≠0)的图象交于A(6,1),B(a,6)两点.
如图,一次函数y=kx+b与反比例函数y=$\frac{m}{x}$(m≠0)的图象交于A(6,1),B(a,6)两点. 在平面直角坐标系xOy中,抛物线y=mx2-2mx+m-1(m>0)与x轴的交点为A,B.
在平面直角坐标系xOy中,抛物线y=mx2-2mx+m-1(m>0)与x轴的交点为A,B.