题目内容
10.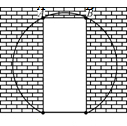 温州外国语学校在进行校园二次美化工程,一面墙上有一个矩形的门洞,如图,已知矩形的高为2米,宽为0.8米,现要将它改为一个圆弧形的门洞,圆弧所在的圆外接于矩形,圆弧所在的圆的半径长为$\frac{2\sqrt{29}}{5}$米.
温州外国语学校在进行校园二次美化工程,一面墙上有一个矩形的门洞,如图,已知矩形的高为2米,宽为0.8米,现要将它改为一个圆弧形的门洞,圆弧所在的圆外接于矩形,圆弧所在的圆的半径长为$\frac{2\sqrt{29}}{5}$米.
分析 先证得BC是直径,在直角三角形BCD中,由BD与CD的长,利用勾股定理求出BC的长,即可求得半径.
解答 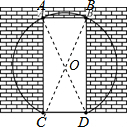 解:如图连结AD、BC,
解:如图连结AD、BC,
∵∠BDC=90°,
∴BC是直径,
∴BC=$\sqrt{B{D}^{2}+C{D}^{2}}$=$\sqrt{{2}^{2}+0.{8}^{2}}$=$\frac{2\sqrt{29}}{5}$,
∴圆形门洞的半径为$\frac{\sqrt{29}}{5}$.
故答案为:$\frac{\sqrt{29}}{5}$.
点评 本题考查了圆周角定理和垂径定理,扇形和三角形的面积,矩形的性质,关键是理解题意.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
5.下列图形是正方体表面积展开图的是( )
| A. |  | B. |  | C. |  | D. |  |
15. 如图,数轴上的A,B,C,D四点中,与表示-$\sqrt{7}$的点最接近的是( )
如图,数轴上的A,B,C,D四点中,与表示-$\sqrt{7}$的点最接近的是( )
 如图,数轴上的A,B,C,D四点中,与表示-$\sqrt{7}$的点最接近的是( )
如图,数轴上的A,B,C,D四点中,与表示-$\sqrt{7}$的点最接近的是( )| A. | 点A | B. | 点B | C. | 点C | D. | 点D |
 某学校教学楼从一楼到二楼由两段坡度相等的楼梯CA、AB联通(如图),经测量的这两层楼间的垂直高度BC为5米,∠BAC=70°,试求一楼到二楼的楼梯总长度(精确到0.1米).
某学校教学楼从一楼到二楼由两段坡度相等的楼梯CA、AB联通(如图),经测量的这两层楼间的垂直高度BC为5米,∠BAC=70°,试求一楼到二楼的楼梯总长度(精确到0.1米).
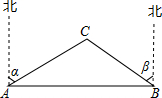 如图,已知A、B两市相距150千米,分别从A、B处测得某风景区中心C处的方向角如图所示,风景区区域是以C为圆心,52千米为半径的圆,tanα≈1.63,tanβ≈1.37.有关部门要设计修建连接AB两市的高速公路,问连接AB的高速公路是否穿过风景区,请说明理由.
如图,已知A、B两市相距150千米,分别从A、B处测得某风景区中心C处的方向角如图所示,风景区区域是以C为圆心,52千米为半径的圆,tanα≈1.63,tanβ≈1.37.有关部门要设计修建连接AB两市的高速公路,问连接AB的高速公路是否穿过风景区,请说明理由.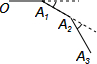 如图,小敏从点0出发,前进10 m到达点A1后,向右转30°前进10m到达点A2,再向
如图,小敏从点0出发,前进10 m到达点A1后,向右转30°前进10m到达点A2,再向