题目内容
已知在△OMN中,OM=ON,∠MON=90°,点B为MN的延长线上一点,OC⊥OB,且OC=OB,OG⊥BC于G,交MN于点A.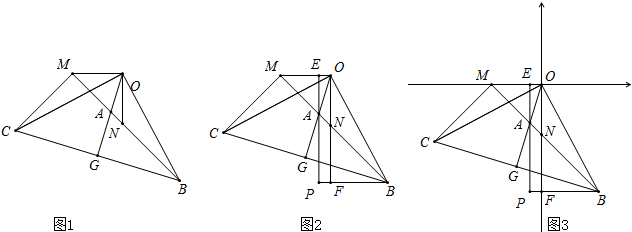
(1)如图1,①求证:∠CMB=90°;
②求证:AM2+BN2=AB2.
(2)如图2,在条件(1)下,过A作AE⊥OM于E,过B作BF⊥ON于F,EA、BF的延长线交于点P,则PA、AE、BF之间的数量关系为 ,△AME、△PAB、△BFN的面积之间的关系为 .
(3)如图3,在条件(2)下,分别以OM、ON为x轴和y轴建立坐标系,双曲线 经过点P,若 y=
经过点P,若MN=2
,求k的值.

(1)如图1,①求证:∠CMB=90°;
②求证:AM2+BN2=AB2.
(2)如图2,在条件(1)下,过A作AE⊥OM于E,过B作BF⊥ON于F,EA、BF的延长线交于点P,则PA、AE、BF之间的数量关系为
(3)如图3,在条件(2)下,分别以OM、ON为x轴和y轴建立坐标系,双曲线 经过点P,若 y=
| k |
| x |
| 2 |
考点:反比例函数综合题
专题:综合题
分析:(1)①由等腰直角三角形的性质得到一对直角相等,再利用等式的性质得到夹角相等,利用SAS得到三角形MOC与三角形NOB全等,利用全等三角形对应角相等得到∠MCO=∠NBO,根据三角形BOD为直角三角形,等量代换即可得证;②连接AC,由三角形MCO与三角形NBO全等,利用全等三角形对应边相等得到BN=CM,在直角三角形AMC中,利用勾股定理列出关系式,等量代换即可得证;
(2)AP2=AE2+BF2,理由为:由题意得到三角形MEA与三角形NFB都为等腰直角三角形,根据等腰直角三角形的性质及勾股定理即可得证;根据题意得到S△BFN+S△AME=S△PAB;
(3)由三角形MON为等腰直角三角形,根据MN的长,利用勾股定理求出OM与ON的长,设P(x,y),x>0,y>0,进而表示出AE=ME=2-x,BF=y-2,PA=y-(2-x),根据AP2=AE2+BF2,得到xy的值,即为k的值.
(2)AP2=AE2+BF2,理由为:由题意得到三角形MEA与三角形NFB都为等腰直角三角形,根据等腰直角三角形的性质及勾股定理即可得证;根据题意得到S△BFN+S△AME=S△PAB;
(3)由三角形MON为等腰直角三角形,根据MN的长,利用勾股定理求出OM与ON的长,设P(x,y),x>0,y>0,进而表示出AE=ME=2-x,BF=y-2,PA=y-(2-x),根据AP2=AE2+BF2,得到xy的值,即为k的值.
解答: (1)①证明:∵∠MON=∠BOC=90°,
(1)①证明:∵∠MON=∠BOC=90°,
∴∠MON-∠CON=∠COB-∠CON,即∠MOC=∠NOB,
在△MOC和△NOB中,
,
∴△MOC≌△NOB(SAS),
∴∠MCO=∠NBO,
在△OBD中,∠ODB+∠NBO=90°,∠ODB=∠MDC,
∴∠MDC+∠MCO=90°,
则∠CMB=90°;
②证明:连接CA,如图所示,
由△MOC≌△NOB,得到BN=CM,
∵△COB为等腰直角三角形,OG⊥BC,
∴AB=AC,
在Rt△CMA中,利用勾股定理得:AM2+CM2=AC2,
∴AM2+BN2=AB2;
(2)解:∵△MON为等腰直角三角形,
∴∠M=45°,
∵AE⊥ON,BF⊥ON,
∴∠MAE=45°,∠B=∠FNB=45°,
∴△MEA和△NFB都为等腰直角三角形,
∴AE2=
AM2,BF2=
BN2,
∴AE2+BF2=
(AM2+BN2)=
AB2,
∵AP2=
AB2,
∴AP2=AE2+BF2;
根据题意得:S△BFN+S△AME=S△PAB;
故答案为:AP2=AE2+BF2;S△BFN+S△AME=S△PAB;
(3)解:∵MN=2
,△OMN为等腰直角三角形,
∴OM=ON=2,
设P(x,y),x>0,y>0,
则AE=ME=2-x,BF=y-2,PA=y-(2-x),
根据AP2=AE2+BF2,得到(x+y-2)2=(2-x)2+(y-2)2,
整理得:xy=2,
则k=xy=2.
 (1)①证明:∵∠MON=∠BOC=90°,
(1)①证明:∵∠MON=∠BOC=90°,∴∠MON-∠CON=∠COB-∠CON,即∠MOC=∠NOB,
在△MOC和△NOB中,
|
∴△MOC≌△NOB(SAS),
∴∠MCO=∠NBO,
在△OBD中,∠ODB+∠NBO=90°,∠ODB=∠MDC,
∴∠MDC+∠MCO=90°,
则∠CMB=90°;
②证明:连接CA,如图所示,
由△MOC≌△NOB,得到BN=CM,
∵△COB为等腰直角三角形,OG⊥BC,
∴AB=AC,
在Rt△CMA中,利用勾股定理得:AM2+CM2=AC2,
∴AM2+BN2=AB2;
(2)解:∵△MON为等腰直角三角形,
∴∠M=45°,
∵AE⊥ON,BF⊥ON,
∴∠MAE=45°,∠B=∠FNB=45°,
∴△MEA和△NFB都为等腰直角三角形,
∴AE2=
| 1 |
| 2 |
| 1 |
| 2 |
∴AE2+BF2=
| 1 |
| 2 |
| 1 |
| 2 |
∵AP2=
| 1 |
| 2 |
∴AP2=AE2+BF2;
根据题意得:S△BFN+S△AME=S△PAB;
故答案为:AP2=AE2+BF2;S△BFN+S△AME=S△PAB;
(3)解:∵MN=2
| 2 |
∴OM=ON=2,
设P(x,y),x>0,y>0,
则AE=ME=2-x,BF=y-2,PA=y-(2-x),
根据AP2=AE2+BF2,得到(x+y-2)2=(2-x)2+(y-2)2,
整理得:xy=2,
则k=xy=2.
点评:此题属于反比例函数综合题,涉及的知识有:全等三角形的判定与性质,等腰直角三角形的判定与性质,勾股定理,熟练掌握判定与性质是解本题的关键.

练习册系列答案
相关题目
一块面积是600m2的长方形土地,它的长比宽多10m,设宽为x,则可列方程为( )
| A、x2-10x+600=0 |
| B、x2+10x-600=0 |
| C、x(x-10)=600 |
| D、x(x+10)+600=0 |
若2x+2y=xy,则
+
的值为( )
| 1 |
| x |
| 1 |
| y |
| A、0 | ||
| B、-1 | ||
C、
| ||
| D、2 |
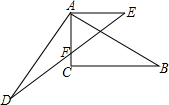 已知如图,AC=AE,AD=AB,∠ACB=∠DAB=90°,AE∥CB,AC、DE交于点F.
已知如图,AC=AE,AD=AB,∠ACB=∠DAB=90°,AE∥CB,AC、DE交于点F.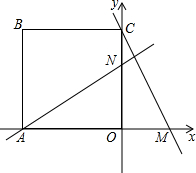 如图,将边长为4的正方形ABCO放置在直角坐标系中,使点A在x轴负半轴上,点C在y轴正半轴上.点M(t,0)在x正半轴上运动,过A作直线MC的垂线交y轴于点N.下列结论:
如图,将边长为4的正方形ABCO放置在直角坐标系中,使点A在x轴负半轴上,点C在y轴正半轴上.点M(t,0)在x正半轴上运动,过A作直线MC的垂线交y轴于点N.下列结论: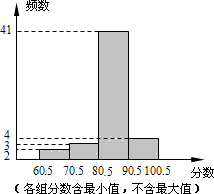 某中学在一次健康知识测试中,抽取部分学生的成绩(分数为整数,满分100分)为样本,绘制成绩统计图如图所示,请结合统计图回答下列问题:
某中学在一次健康知识测试中,抽取部分学生的成绩(分数为整数,满分100分)为样本,绘制成绩统计图如图所示,请结合统计图回答下列问题: