题目内容
解下列方程:
(1)8-3y=5y-16
(2)5(x+8)=6(2x-7)+5;
(3)
=
(4)
-
=1
(5)
=
.
(1)8-3y=5y-16
(2)5(x+8)=6(2x-7)+5;
(3)
| 3y+5 |
| 2 |
| 2y-1 |
| 3 |
(4)
| x+2 |
| 4 |
| 2x-3 |
| 6 |
(5)
| y-3 |
| -5 |
| 3y+4 |
| 15 |
考点:解一元一次方程
专题:
分析:(1)移项、合并同类项,系数化成1即可求解;
(2)去括号、移项、合并同类项、系数化成1即可求解;
(3)去分母、去括号、移项、合并同类项、系数化成1即可求解;
(4)去分母、去括号、移项、合并同类项、系数化成1即可求解;
(5)去分母、去括号、移项、合并同类项、系数化成1即可求解.
(2)去括号、移项、合并同类项、系数化成1即可求解;
(3)去分母、去括号、移项、合并同类项、系数化成1即可求解;
(4)去分母、去括号、移项、合并同类项、系数化成1即可求解;
(5)去分母、去括号、移项、合并同类项、系数化成1即可求解.
解答:解:(1)移项,得-3y-5y=-16-8,
合并同类项,得:-8y=-24,
系数化成1得:y=3;
(2)去括号,得:5x+40=12x-42+5,
移项,得:5x-12x=-42+5-40,
合并同类项,得:-7x=-77,
系数化为1得:x=11;
(3)3(3y+5)=2(2y-1),
去括号,得:9y+15=4y-2,
合并同类项,得:9y-4y=-2-15,
合并同类项,得:5y=-17,
系数化为1得:y=-
;
(4)去分母,得:6(x+2)-4(2x-3)=24,
去括号,得:6x+12-8x+12=24,
移项,得:6x-8x=24-12-12,
合并同类项,得:-2x=0,
系数化成1得:x=0;
(5)去分母,得:3(y-3)=-3y-4,
去括号,得:3y-9=-3y-4,
移项,得:3y+3y=-4+9,
合并同类项,得:6y=5,
系数化成1得:y=
.
合并同类项,得:-8y=-24,
系数化成1得:y=3;
(2)去括号,得:5x+40=12x-42+5,
移项,得:5x-12x=-42+5-40,
合并同类项,得:-7x=-77,
系数化为1得:x=11;
(3)3(3y+5)=2(2y-1),
去括号,得:9y+15=4y-2,
合并同类项,得:9y-4y=-2-15,
合并同类项,得:5y=-17,
系数化为1得:y=-
| 17 |
| 5 |
(4)去分母,得:6(x+2)-4(2x-3)=24,
去括号,得:6x+12-8x+12=24,
移项,得:6x-8x=24-12-12,
合并同类项,得:-2x=0,
系数化成1得:x=0;
(5)去分母,得:3(y-3)=-3y-4,
去括号,得:3y-9=-3y-4,
移项,得:3y+3y=-4+9,
合并同类项,得:6y=5,
系数化成1得:y=
| 5 |
| 6 |
点评:本题考查解一元一次方程,解一元一次方程的一般步骤是:去分母、去括号、移项、合并同类项、化系数为1.注意移项要变号.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
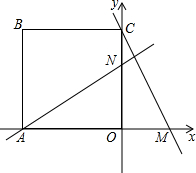 如图,将边长为4的正方形ABCO放置在直角坐标系中,使点A在x轴负半轴上,点C在y轴正半轴上.点M(t,0)在x正半轴上运动,过A作直线MC的垂线交y轴于点N.下列结论:
如图,将边长为4的正方形ABCO放置在直角坐标系中,使点A在x轴负半轴上,点C在y轴正半轴上.点M(t,0)在x正半轴上运动,过A作直线MC的垂线交y轴于点N.下列结论: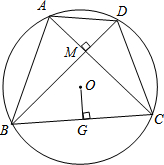 已知:圆的内接四边形ABCD的对角线AC和BD互相垂直,OG⊥BC,求证:OG=
已知:圆的内接四边形ABCD的对角线AC和BD互相垂直,OG⊥BC,求证:OG=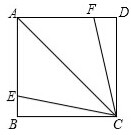 如图,AC是正方形ABCD的对角线,E、F分别为AB、AD边上的点,且AE=AF,连接CE、CF.
如图,AC是正方形ABCD的对角线,E、F分别为AB、AD边上的点,且AE=AF,连接CE、CF. 如图,在矩形ABCD中,对角线AC,BD交于点O.已知∠AOB=60°,AB=4,求矩形的面积.
如图,在矩形ABCD中,对角线AC,BD交于点O.已知∠AOB=60°,AB=4,求矩形的面积.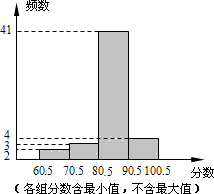 某中学在一次健康知识测试中,抽取部分学生的成绩(分数为整数,满分100分)为样本,绘制成绩统计图如图所示,请结合统计图回答下列问题:
某中学在一次健康知识测试中,抽取部分学生的成绩(分数为整数,满分100分)为样本,绘制成绩统计图如图所示,请结合统计图回答下列问题: