题目内容
19.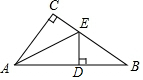 如图,已知在△ABC中,∠C=90°,AD=AC,DE⊥AB交BC于点E,若∠B=26°,则∠AEC=( )
如图,已知在△ABC中,∠C=90°,AD=AC,DE⊥AB交BC于点E,若∠B=26°,则∠AEC=( )| A. | 26° | B. | 32° | C. | 58° | D. | 64° |
分析 根据∠C=90°,AD=AC求证Rt△CAE≌Rt△DAE,∠CAE=∠DAE=$\frac{1}{2}$∠CAB,再由∠C=90°,∠B=26°,求出∠CAB的度数,然后即可求出∠AEC的度数.
解答 解:∵在△ABC中,∠C=90°,DE⊥AB交BC于点E,
∴∠ADE=∠C=90°,
在Rt△ACE和Rt△ADE中,
∵$\left\{\begin{array}{l}{AC=AD}\\{AE=AE}\end{array}\right.$,
∴Rt△CAE≌Rt△DAE,
∴∠CAE=∠DAE=$\frac{1}{2}$∠CAB,
∵∠B+∠CAB=90°,∠B=26°,
∴∠CAB=90°-26°=64°,
∵∠AEC=90°-$\frac{1}{2}$∠CAB=90°-32°=58°.
故选:C
点评 此题主要考查学生对直角三角形全等的判定和三角形内角和定理的理解和掌握,解答此题的关键是求证Rt△CAE≌Rt△DAE.

练习册系列答案
相关题目
7.如图1,在等边△ABC中,动点P从点A出发,沿三角形的边由A→C→B作匀速运动,设点P运动的路程为x,△ABP的面积为y,把y看作x的函数,函数的图象如图2所示,则△ABC的面积为( )


| A. | 4$\sqrt{3}$ | B. | 8$\sqrt{3}$ | C. | 8 | D. | 16 |
11.已知mn≠1,且5m2+2010m+9=0,9n2+2010n+5=0,则$\frac{m}{n}$的值为( )
| A. | -402 | B. | $\frac{5}{9}$ | C. | $\frac{9}{5}$ | D. | $\frac{670}{3}$ |
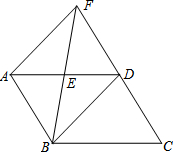 如图,在□ABCD中,E是AD边上的中点,连接BE,并延长BE交CD的延长线于点F,连接BD、AF,BE平分∠ABD,∠ABD=60°.
如图,在□ABCD中,E是AD边上的中点,连接BE,并延长BE交CD的延长线于点F,连接BD、AF,BE平分∠ABD,∠ABD=60°. 若画图并填空:
若画图并填空: 如图,在正方形ABCD中,有一个面积为25的小正方形EFGH,其中E、F、G、H分别在AB、BC、FD上,若BF=4,则AB的长为( )
如图,在正方形ABCD中,有一个面积为25的小正方形EFGH,其中E、F、G、H分别在AB、BC、FD上,若BF=4,则AB的长为( )