题目内容
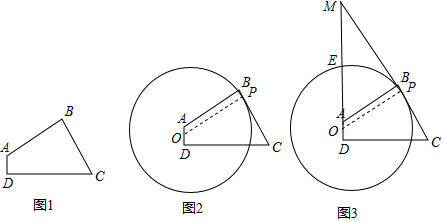
7.如图1,在等边△ABC中,动点P从点A出发,沿三角形的边由A→C→B作匀速运动,设点P运动的路程为x,△ABP的面积为y,把y看作x的函数,函数的图象如图2所示,则△ABC的面积为( )
| A. | 4$\sqrt{3}$ | B. | 8$\sqrt{3}$ | C. | 8 | D. | 16 |
分析 根据图2可得:等边三角形的边长为4,根据三角形的特殊角的三角函数求高AD的长,由三角形面积可得结论.
解答  解:由图2可知:等边三角形的边长为4,
解:由图2可知:等边三角形的边长为4,
如图3,作高AD,
∴AC=4,∠C=60°,
sin60°=$\frac{AD}{AC}$,
AD=ACsin60°=4×$\frac{\sqrt{3}}{2}$=2$\sqrt{3}$,
∴y=$\frac{1}{2}$BC•AD=$\frac{1}{2}$×4×2$\sqrt{3}$=4$\sqrt{3}$.
故选A.
点评 本题考查了动点问题的函数图象,从图象中通过确定点P与C重合时的位置得到等边三角形的边长是关键.

练习册系列答案
相关题目
19.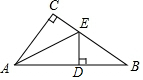 如图,已知在△ABC中,∠C=90°,AD=AC,DE⊥AB交BC于点E,若∠B=26°,则∠AEC=( )
如图,已知在△ABC中,∠C=90°,AD=AC,DE⊥AB交BC于点E,若∠B=26°,则∠AEC=( )
 如图,已知在△ABC中,∠C=90°,AD=AC,DE⊥AB交BC于点E,若∠B=26°,则∠AEC=( )
如图,已知在△ABC中,∠C=90°,AD=AC,DE⊥AB交BC于点E,若∠B=26°,则∠AEC=( )| A. | 26° | B. | 32° | C. | 58° | D. | 64° |
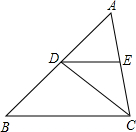 已知:如图,CD平分∠ACB,DE∥BC,∠AED=80°.求∠EDC.
已知:如图,CD平分∠ACB,DE∥BC,∠AED=80°.求∠EDC. 如图,AB⊥BD于点B,CD⊥BD于点D,∠1+∠2=180°,试说明:CD∥EF
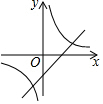
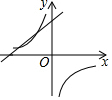
如图,AB⊥BD于点B,CD⊥BD于点D,∠1+∠2=180°,试说明:CD∥EF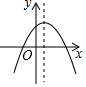 已知二次函数y=ax2+bx+c的图象如图,在同一直角坐标系中,一次函数y=cx+a和反比例函数y=$\frac{b}{x}$的图象大致是( )
已知二次函数y=ax2+bx+c的图象如图,在同一直角坐标系中,一次函数y=cx+a和反比例函数y=$\frac{b}{x}$的图象大致是( )