题目内容
8.某农贸市场欲购进A、B两种产品进行销售,已知A种农产品进价50元/斤,B种农产品进价70元/斤(1)如果购进A、B两种农产品共60斤花费3400元,求A、B两种农产品各购进多少斤
(2)如果至少购进A、B两种农产品共80斤,花费4800元
①设购进A种农产品a斤,则购进B种农产品(80-a)斤
②在①的基础上求出A种农产品最少购进多少斤?
分析 (1)设A、B两种农产品各购进x斤,y斤,根据购进A、B两种农产品共60斤花费3400元,列方程组求解即可;
(2)假设购进A种农产品a斤,则购进B种农产品(80-a)斤,依据购进A、B两种农产品共花费4800元,列不等式即可得到A种农产品最少购进的斤数.
解答 解:(1)设A、B两种农产品各购进x斤,y斤,根据题意得,
$\left\{\begin{array}{l}{x+y=60}\\{50x+70y=3400}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=40}\\{y=20}\end{array}\right.$,
答:A、B两种农产品各购进40斤,20斤;
(2)①购进A种农产品a斤,则购进B种农产品(80-a)斤,
故答案为:(80-a);
②由题意得,50a+70(80-a)≤4800,
解得:a≥40,
∴A种农产品最少购进40斤.
点评 本题主要考查了一元一次不等式依据二元一次方程的应用,解题时注意:当问题较复杂时,有时设与要求的未知量相关的另一些量为未知数,即为间接设元.无论怎样设元,设几个未知数,就要列几个方程.列不等式解应用题需要以“至少”、“最多”、“不超过”、“不低于”等词来体现问题中的不等关系.

练习册系列答案
相关题目
19.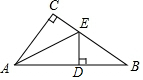 如图,已知在△ABC中,∠C=90°,AD=AC,DE⊥AB交BC于点E,若∠B=26°,则∠AEC=( )
如图,已知在△ABC中,∠C=90°,AD=AC,DE⊥AB交BC于点E,若∠B=26°,则∠AEC=( )
 如图,已知在△ABC中,∠C=90°,AD=AC,DE⊥AB交BC于点E,若∠B=26°,则∠AEC=( )
如图,已知在△ABC中,∠C=90°,AD=AC,DE⊥AB交BC于点E,若∠B=26°,则∠AEC=( )| A. | 26° | B. | 32° | C. | 58° | D. | 64° |
20. 如图可以近似地刻画下述哪个情景( )
如图可以近似地刻画下述哪个情景( )
 如图可以近似地刻画下述哪个情景( )
如图可以近似地刻画下述哪个情景( )| A. | 小明匀速步行上学(离学校的距离与时间的关系) | |
| B. | 匀速行驶的汽车(速度与时间的关系) | |
| C. | 小亮妈到超市购买苹果(总费用与重量的关系) | |
| D. | 一个匀速上升的气球(高度与时间的关系) |
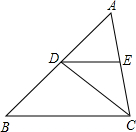 已知:如图,CD平分∠ACB,DE∥BC,∠AED=80°.求∠EDC.
已知:如图,CD平分∠ACB,DE∥BC,∠AED=80°.求∠EDC.
 如图,直线AB、CD被直线MN所截,当添加条件∠AEF=∠CFE时,AB∥CD.(只要写出一个你认为适合的条件即可)
如图,直线AB、CD被直线MN所截,当添加条件∠AEF=∠CFE时,AB∥CD.(只要写出一个你认为适合的条件即可)