题目内容
4. 如图,在正方形ABCD中,有一个面积为25的小正方形EFGH,其中E、F、G、H分别在AB、BC、FD上,若BF=4,则AB的长为( )
如图,在正方形ABCD中,有一个面积为25的小正方形EFGH,其中E、F、G、H分别在AB、BC、FD上,若BF=4,则AB的长为( )| A. | 16 | B. | 15 | C. | 13 | D. | 12 |
分析 易求小正方形EFGH,结合正方形的性质和勾股定理可求出BE的长,再根据相似三角形的判定定理得出△BEF∽△CFD,由相似三角形的对应边成比例即可求出AB的长.
解答 解:
∵小正方形EFGH的面积为25,
∴EF=5,
∵四边形ABCD是正方形,
∴∠B=90°, BC=DC,
BC=DC,
∵BF=4,
∴BE=$\sqrt{E{F}^{2}-B{F}^{2}}$=3,
在△BEF与△CFD中,
∵∠1+∠2=∠2+∠3=90°,
∴∠1=∠3
∵∠B=∠C=90°,
∴△BEF∽△CFD,
∴$\frac{BF}{DC}=\frac{BE}{CF}$,
设CD=BC=x,则CF=x-4,
∴$\frac{4}{x}=\frac{3}{x-4}$,
解得:x=16,
∴AB=16,
故选A.
点评 本题考查的是正方形的性质、相似三角形的判定与性质及勾股定理的运用,根据题意得出△BEF∽△CFD是解答此题的关键.

练习册系列答案
相关题目
19.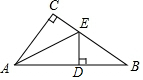 如图,已知在△ABC中,∠C=90°,AD=AC,DE⊥AB交BC于点E,若∠B=26°,则∠AEC=( )
如图,已知在△ABC中,∠C=90°,AD=AC,DE⊥AB交BC于点E,若∠B=26°,则∠AEC=( )
 如图,已知在△ABC中,∠C=90°,AD=AC,DE⊥AB交BC于点E,若∠B=26°,则∠AEC=( )
如图,已知在△ABC中,∠C=90°,AD=AC,DE⊥AB交BC于点E,若∠B=26°,则∠AEC=( )| A. | 26° | B. | 32° | C. | 58° | D. | 64° |
9.有一个边长为40cm的正方形洞口,要用一个圆盖去盖住这个洞口,那么圆盖的直径至少应为( )
| A. | 40cm | B. | 20$\sqrt{2}$cm | C. | 40$\sqrt{2}$cm | D. | 40$\sqrt{3}$cm |
 如图,AB⊥BD于点B,CD⊥BD于点D,∠1+∠2=180°,试说明:CD∥EF
如图,AB⊥BD于点B,CD⊥BD于点D,∠1+∠2=180°,试说明:CD∥EF



 如图,直线AB、CD被直线MN所截,当添加条件∠AEF=∠CFE时,AB∥CD.(只要写出一个你认为适合的条件即可)
如图,直线AB、CD被直线MN所截,当添加条件∠AEF=∠CFE时,AB∥CD.(只要写出一个你认为适合的条件即可)