Question

1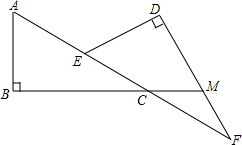．如图．在Rt△ABC和Rt△DEF中，∠B=∠D=90°，点A．E．C．F在同一直线上，AE=CF，BC的延长线交DF于点M．∠MCF=∠F，求证：BC=DF．

Answer 1

分析 根据等式的性质，可得AC与EF的关系，根据对顶角的性质，可得∠MCF与∠ACB的关系，根据等腰三角形的判定与性质，可得答案．

解答 证明：∵AE=CF，
∴AE+CE=CF+CE，即AC=EF．
∵∠MCF与∠ACB是对顶角，
∴∠MCF=∠ACB．
又∵∠MCF=∠F，
∴∠ACB=∠F．
在Rt△ABC和Rt△EDF中，
$\left\{\begin{array}{l}{∠ACB=∠F}\\{∠ABC=∠EDF}\\{AC=EF}\end{array}\right.$，
∴Rt△ABC≌Rt△EDF（AAS），
∴BC=DF．

点评 本题考查了全等三角形的判定与性质，利用等式的性质得出AC=EF是解题关键，又利用了全等三角形的判定与性质．